わかった気になるマトリックス

2013/7/8

Tag: maya,tips

お初にお目にかかります。TD の土屋と申します。

さて、何かテクニカルなネタを書かなければいけないらしいんですが、私はこの会社に来て日も浅いので、
そういう意味ではこれといってお披露目するようなものもございません。
過去をふりかえればネタはないこともないのですが、外でやったことはどこかの誰かに叱られる可能性もなくもないような。

といったところで、今回は「行列＝マトリックス」の基礎的な扱い方について記事を書いてみることにしました。
目を背けがちな「マトリックス」に親しみを持ってもらい、Maya を使う上で少し役立つかもしれないような記事を
目指します。

---

デザイナーさんに何か技術的な質問などをされた際に、
「ここのマトリックスが・・・・」みたいな説明をしようものなら渋い顔をされることうけあいです。
マトリックス・アレルギーとも言える状態・・・「マトリックス」という単語を使うこと自体、タブーですか。そうですか。
・・・みたいなことも、何度かありました。
＊＊＊
マトリックスのことを調べようとすると「行列のルールはこうで数学的にはこんな性質が」という説明ばかりが出てきて、
現実との接点が見出せずに諦めていないでしょうか。
記事ではMayaでの実例を交えながら、私なりの理解をもとに、なるべく専門用語やわかりにくい表記を排除して説明して
いくつもりです。

なんだかんだで結構なボリュームになりそうなので、以下の内容で３回程に分けてお送りする予定です。
（内容は変更になる場合があります）。

【第一回（今回）】
●Transform ノードのアトリビュートとマトリックス ●座標変換の考え方
●座標軸で３×３マトリックスを組み立ててみる ●座標変換の方法
【第二回】
●translate の組み込み（4×4マトリックスへ拡張） ●マトリックス合成の理屈と方法
●Transform ノード各要素のマトリックスの作成（rotate と三角関数の解説、その他の要素の解説）
【第三回】
●座標軸をロケーターでコントロールするデモ ●ジオメトリとマトリックス
●逆マトリックス ●Transform ノードのマトリックス出力

---

＊＊＊　では、ここからスタートです！　＊＊＊

さて、Mayaで座標変換のマトリックスはどのような役回りを演じているでしょうか？

・・・・その前に、座標を変換するとはどういうことを指すでしょうか？
もっとも身近なところでは、Transform や Joint に移動や回転などの値を入力し、その子供になっているオブジェクトの
位置や角度を設定するということがその１つにあたります。
Joint は Transform とアトリビュート（パラメーター）が異なるため使い方は違いますが、やっていることはそんなに
変わりません。Transform をカスタマイズしたようなものなので、Joint のことはいったん忘れます。

１つの Transform 内の座標変換に直接かかわるアトリビュートを調べてみると、結構たくさんあることがわかります。

【アトリビュートエディターで編集できる Transform ノードのパラメーター】

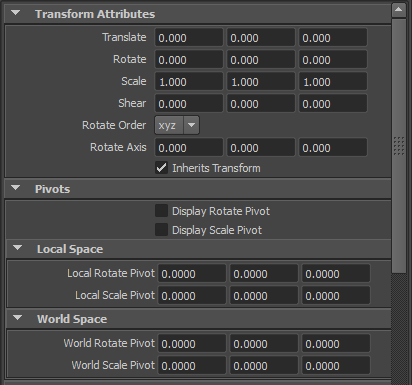
【Transform ノードのアトリビュート】

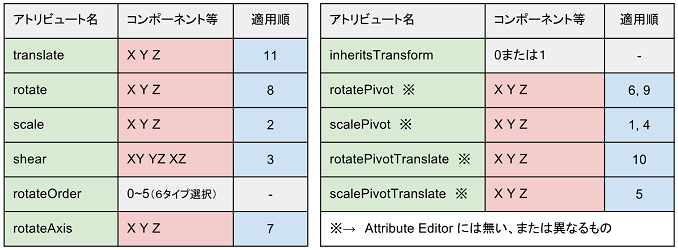
上の表はアトリビュートエディター（UI）のパラメーター表示順にならったものにしてありますが、アトリビュートエディターと
若干違うところや、普段見慣れないものがありますね。
表の上のアトリビュートエディターの画像と比較してみてください。

↓下の枠内は、今回の解説には直接は関係ないですが、参考までに。

★最後の２つ、rotatePivotTranslate と scalePivotTranslate はアトリビュートエディターにはありません 　（これらはツールやオペレーションにより、こっそり値が設定されることがあり、注意が必要）。 ↓Attribute Spread Sheet の All タブでアクセスできます。 ★rotatePivot,　scalePivot はアトリビュートエディターでは、 　それぞれ「Local Rotate Pivot」、「Local Scale Pivot」 にあたります。 ★アトリビュートエディターの「World Space」の中のパラメーターに直接対応するアトリビュートはありません。 　ここに値を設定すると、変換されて Local の値として保存されるしくみになっています。

　

上の表で注目してほしいのは、「X Y Z」、「XY YZ ZX」の表記のあるアトリビュートと「適用順」の数値です。
移動、回転、スケール、などの全ての行程は、実行する順番が変われば座標変換の結果も変わりますが、
この順番は不変で、「適用順」のところにその順番が書いてあります。

↓「適用順」が感覚的に理解しにくい方は、こちらの説明をどうぞ。

例えば、あるオブジェクトを原点に作成して、移動、回転を用いて任意の位置に配置するとします。移動、回転は何度でも、 好きな順番で行って修正できますよね。このとき、Maya が行う 移動、回転の処理は、その時々に設定されている アトリビュートの値をいつも同じ手順で読み取って、同じ順番で計算しなおすだけです。肝心なことは、移動、回転などの １つ１つの処理は、常にそのTransform の親の座標系の「原点を基準に」しか行わない、ということです。 例えば、パラメーターの設定が 　　Translate:10,0,0 Rotate:0,45,0 であれば、Maya は必ず、 　　（親の原点基準で）Rotate:0,45,0 を適用　→　Translate:10,0,0 を適用 という順で処理します（もしくは、そのように処理したかのような結果を出力します）。 適用順は、Rotate→Translate ということになります。もしこれが逆だったとすると、 　　Translate:10,0,0 を適用　→　（親の原点基準で）Rotate:0,45,0 を適用 となり、物体は移動後に原点中心で大きく振られ、結果は全く異なります。 transform ノードには他にもいろいろ要素があるので、それらの処理の順番を示したのが、表の「適用順」です。

　
「適用順」に２つ数字が書いてあるものは、１つめは「反転」され、２つめと打ち消しあうような形で、計２度適用されます
（詳しくは別の機会に解説します）。

translate （平行移動） が１１番目で、一番最後なのがわかりますね。

こうしてみると、沢山数値があって、座標を変換する計算コストも大変そうに見えます。
ポリゴン Shape オブジェクトが Transform の子供になっているなら、Maya はあらゆる場面の処理で、
各頂点の座標に対して変換の全ての要素を適用しなければなりません。

---

ここで、マトリックスの出番です。
マトリックスのデータは、変換に必要な複数のデータを、計算によってひとまとめにすることで、サイズの決まった一組の
数列（行と列）で表現することができます。
このひとまとめにする行程は、Transform のパラメーターの値が決まった時（変化した時）ごとに、一回だけ行えば良いです。
出来上がったマトリックスを Shape の各頂点に適用すれば、その Shape の座標変換は完了します。
結果的に、先ほど心配していた計算量よりはるかに少ない計算で済みます。

マトリックスの利点が１つ見えたところで、なぜ各変換の行程を１つのマトリックスで表現することが可能なのか、
考えてみます。

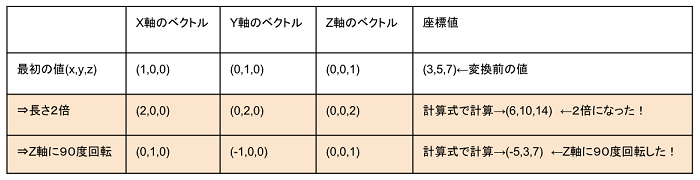
まず、３D 空間内に点を一つ定義します。座標値は（３，５，７）としましょう。
説明のために、この座標を、あえて冗長に定義してみます。

点を定義したこの空間には、X,Y,Z の３つの座標軸がありますよね。これらをそれぞれのベクトルに見立てます。
原点から見て、プラス方向として、全部長さが１とすると、
　　X軸は　（１，０，０）の方向ベクトル
　　Y軸は　（０，１，０）の方向ベクトル
　　Z軸は　（０，０，１）の方向ベクトル
となります。
さてここで、原点を出発点として、これらのベクトルの組み合わせで、全てのベクトルの方向はそのまま、
長さだけを変更して、先程の座標（３，５、７）を指すためには、
　　X方向のベクトルを３倍
　　Y方向のベクトルを５倍
　　Z方向のベクトルを７倍
して順に繋ぎあわせます（一言で言えば「ベクトルの和」ですね）。
繋ぎ合わせの順番は何でも結果は同じですが、最後のベクトルの先端は、先ほどの点の座標を示しているはずです。

【ベクトルの和】　左も右も同じベクトル。

計算式っぽく表現すると、
　　３×（１，０，０）　＋　５×（０，１，０）　＋　７×（０，０，１）　　　　←　座標（３，５，７）を冗長にした表現！
となるのですが、わかるでしょうか？　そしてさらにまとめてみると、
　　⇒（３，０，０）　＋　（０，５，０）　＋　（０，０，７）
　　⇒（３，５，７）
最後は Ｘ，Ｙ，Ｚ ごとに値を足すと、到達地点の座標値になることがわかります。　あたりまえすぎますか？

---

では、もしここで、座標軸を示していた（長さ１だった）最初の３つのベクトルの値を変えてしまったらどうでしょうか。
３つのベクトルを３つとも同じ条件で変更してみます。

座標は最初のまま、（３，５，７）にします。座標値の計算式は、
　　３×（X軸のベクトル）　＋　５×（Y軸のベクトル）　＋　７×（Z軸のベクトル）
です。

【Ｚ軸で９０度回転してみた図】　　左：回転前　　右：回転後

回転といっても９０度なら計算しなくても正解が確認できますよね？
上の表では軸ベクトルに倍率および回転をかけてみたわけですが、結果の座標も同様に変化しました。
これは点を定義した座標軸のベクトル値を変更することで、新しい点の位置を計算できることを示しています。
上の例では、垂直、水平のベクトルですが、実はどんな斜めの方向でも大丈夫です。
３つのベクトルは一緒に回転やスケールをかけても、またばらばらに動かしても、期待したとおりになります。
この場合、軸同士のなす角度が直角以外になると、shear（せん断変形） がかかることになりますね。
この３つの軸のベクトルをうまく定義することで、任意の scale、rotate、shear を表現できそうです
（具体的なベクトルの設定のやり方は、別途説明します）。

そして、これらベクトルの値は、そっくりそのままマトリックスに組み込めます・・・・というわけで、
ここでマトリックスの話に戻ります。
数値データをマトリックスの形にすると、手順はより機械的になりますが、上記の計算と全く同じ計算ができます。

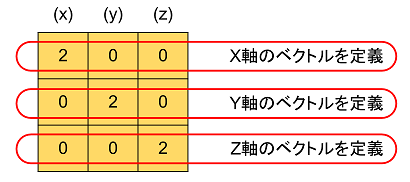
次の図のように、３つのベクトル　×　各ベクトルのｘｙｚの３つの値　＝　９個の数値で、３×３マトリックスを組みます。
数値の並べ方は「ルール」なので、こういうものだ、と思ってください。

例として、軸の値は、上の表の「長さ２倍」の値にしてみます。

さて、マトリックスが１つ組めたところで、このマトリックスを使って座標変換をしてみましょう。
ここではマトリックス同士の「積」を計算します。「積」と言うからには２つのものが必要です。
上で作成したマトリックスと、もう１つは変換する座標値を使って作るマトリックスです。
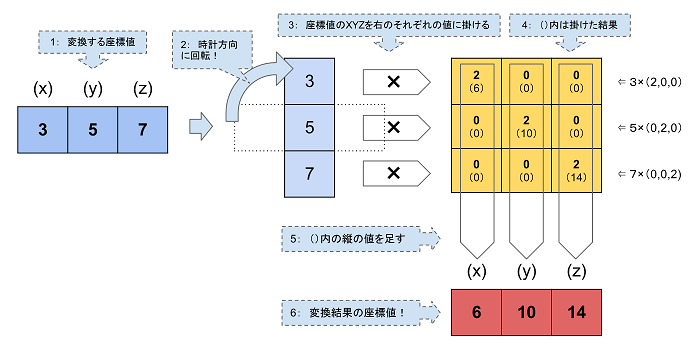
先ほどから使っている（３，５，７）の座標を横に並べてマトリックスにします。
できるのは ３×１ のマトリックスです（１行なのでマトリックスに見えないかもしれませんが）。

そしてさっき作成した座標変換用マトリックスも持ってきて右側に置きます。並べたらすぐ、「積」の計算ができます。
ルールに従って計算していきます。下の図のとおりに計算してみてください。
　・入力座標値のマトリックスの値は一時的に縦に並べ替えます。
　・それらの３つの値を変換マトリックスのほうの横の要素とそれぞれ掛け合わせます。　
　　　↓図では３×３マトリックス内の（）に結果を書きました。
　・その結果を縦の列ごとに足し算をして、完了です。

この例では、各軸方向にスケール２がかかっています。

この計算の結果は、上の表のところで計算した結果と同じですね。マトリックス計算という形式に変わりはしましたが、
計算の内容は全く同じなので、当然同じ答えになります。
「Ｚ軸で９０度回転」のほうも、マトリックスを作成して同じ行程を試してみてください。
また座標や座標軸ベクトルをいろいろ変更して試してみてもいいですね。

ちょっと中途半端ですが、今回はここまでです。お疲れ様でした。
でも、何で３×３なの？４×４じゃないのぉ？　とお思いの方もいると思います。
４×４への拡張は次回お送りする予定です。

※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください