わかった気になるマトリックス　第３回

2014/2/3

Tag: matrix,maya,tips,transform

おひさしぶりです。土屋@TDです。

さて、マトリックス３回目の記事です。
前回、前々回と主にMayaにおける座標変換マトリックスについて自己流で解説してきましたが、
ここまでの内容は納得していただけましたでしょうか・・？
まぁ、これといった苦情等も私の耳には聞こえて来てませんので、今回もペースを崩さず行こうかと思っている次第です。
３回目ですが、もちろん今回では終わりません・・・。

「わかった気になるマトリックス」（第１回）
「わかった気になるマトリックス　第２回」

前回までで Transform ノードのマトリックスの基本的なしくみと、Scale, Rotate, Translate までを解説してきました。
Rotate の解説はちょっと苦しかったかもしれませんが、とりあえず良しとしてください（汗

あと Transform の要素で残っているのは、Shear と、Pivot です。
今回は、マトリックスの合成の解説もしなければいけません。前回の記事で「次回にまわす」って書いていますし。
最初の予定と若干ズレてきていますが、気にせずゴール（？）を目指してやっていくことにします！

【　Shear について　】

気合いが入ったところでなんですが、一般には使用頻度が少ないと思われるせん断変形（Shear・シアー）についての解説から
はじめます・・（以降、”Shear” と表記）。

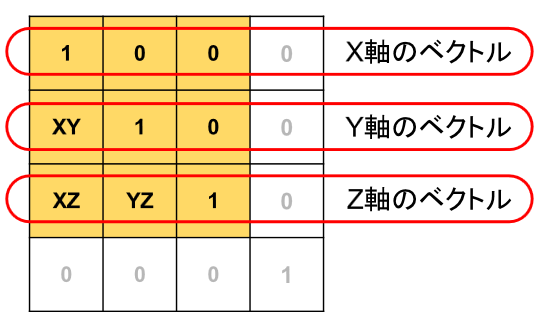
これまでの解説で変換マトリックス内には、３D空間を定義するための、X軸、Y軸、Z軸のベクトルの値が
設定されていると考えました。
Shear の要素のない通常の状態は、これら３つのベクトルは、この中のどの２つをとっても
空間内でそれぞれ90度の角度を維持しています。
逆に言うと90度を保つのをやめたところで、Shear のある状態になり、歪んだ空間を表すことになります。

Attribute Editor 上では、Shear のパラメーターは3つの値で表示されます。

対応するアトリビュート名はそれぞれ、
　　　　shearXY　　shearXZ　　shearYZ　
となっています。そしてMayaでのマトリックスにおける Shear の定義は次のようになっています（”shear” は省略）。

ここまでのマトリックスの解説にあてはめると、上記のパラメーターは、Ｘ軸ベクトルは変化させず、
Ｙ軸とＺ軸のベクトルをデフォルトの方向からずらす効果をもたらすと言えます。
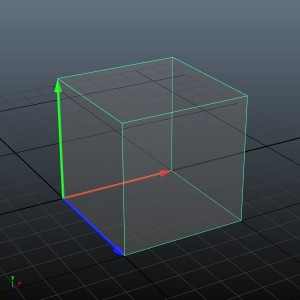
例として、shearXY にパラメーターを設定して、Y軸を少し斜めに変更したのが次の図です
（右の図の小さい矢印が shearXY による変化分）。

上のマトリックスの図をもういちど見てください。
マトリックスの色がぬってある領域の中の右上のほうの領域は0になっているだけで値は設定できません。

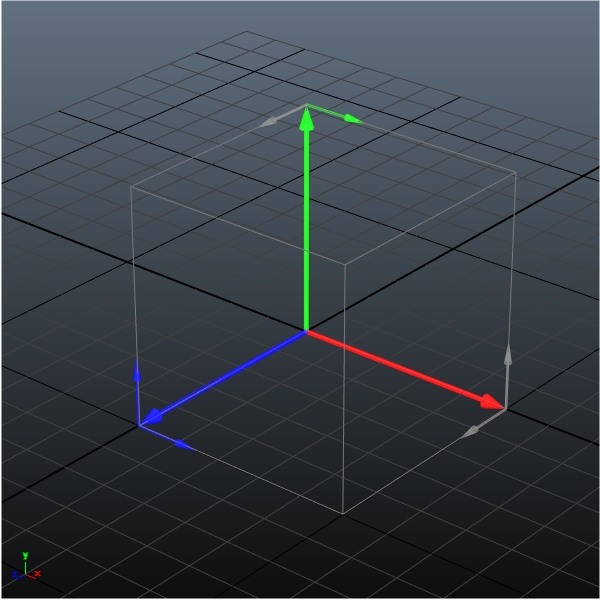
下の図の短い矢印が軸を変化させるためのパラメーターを設定する方向ですが、
グレーの矢印方向にはマトリックス内の座標軸をずらすことはできません。

これを見ると、これはZ軸のための仕様にも思えてきます（ShearXY がおまけっぽく見えます）。
もしもグレーの方向に座標軸をずらしたいなら、その軸をZ軸に合わせるために、別階層の Transform で全体を回転した上で
Shear を設定できるような構造を作るなど、工夫が必要です。
実は Scale と Rotate のパラメーターを併用していいならグレー方向の Shear の効果をもたらす変換はつくれるのですが、
パラメーターの生成のための計算が伴いますし、普通はやろうとは思わないでしょう。
ただ、逆に言えば、この３つのパラメーターがあれば、あらゆる Shear の状態を１つの Transform で表現することは
可能ということでもあり、そういう意味では必要十分ということもできます。
全方向の Shear をストレートにパラメーターの設定で可能にするとなると、パラメーターが6個も必要になるので、
仕様的にそれを避けたのかもしれません（・・・私がこだわり過ぎなだけなんでしょうか？）。
今の仕様になってるのは、Shear自体の使用頻度が少ないのと、CAD 時代の仕様を引き継いでいるとか、
歴史的な背景もあるのかもしれませんね。

Shear についてはもう少し掘り下げられなくもないですが、これぐらいにしておきましょう・・次は Pivot です。

【　Pivotについて　】

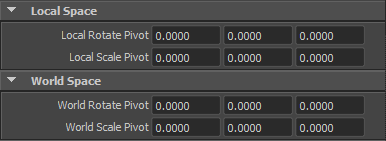
Attribute Editor 上で、Pivot はX,Y,Z の値（座標値）で表示されます。
第１回でちょっと触れたのですが、Transform ノードの Pivot 設定 には、”rotatePivot” と “scalePivot” の２組の
アトリビュートがあり、これは Attribute Editor の 「Local Space」 の Pivot のパラメーターに相当します。

（↓Attribute Editor の表示）

「World Space」 の数値フィールドもありますが、これは Local の値との相互変換を行っていて、Transform ノード側では
Local の数値のみを保持しています。Local が実体、World は投影された値です。
アトリビュート名は次のようになっています。

(Rotate):　　rotatePivotX　　rotatePivotY　　roatePivotZ
(Scale):　　scalePivotX　　scalePivotY　　scalePivotZ

ここで注意しなければならないことがあります！！

第１回でもちょっと出てきましたが、Pivot には上記のそれぞれのアトリビュートに対応した「裏アトリビュート」（？）が
存在します（上記のアトリビュート名の “—Pivot” のうしろに ”Translate” がついた名称のアトリビュート）。
通常、Transform ノードの各パラメーターが初期値の場合は、Pivot 値を変更しても、見た目上は変わりません。
では、例として、Scale に 1 以外の数値を設定した状態から、 Pivot の値を変更したとするとどうでしょうか？
Scale の基準点が変わった状態で Scale の変換が行われるので、見た目も変化するはずです。

しかし Attribute Editor や View 上で Pivot を変更しても実際にはそうなりません。
これは、見た目が変化しないように、「裏アトリビュート」にその変化分を相殺するための値（移動値）が自動的に
設定されるからです。

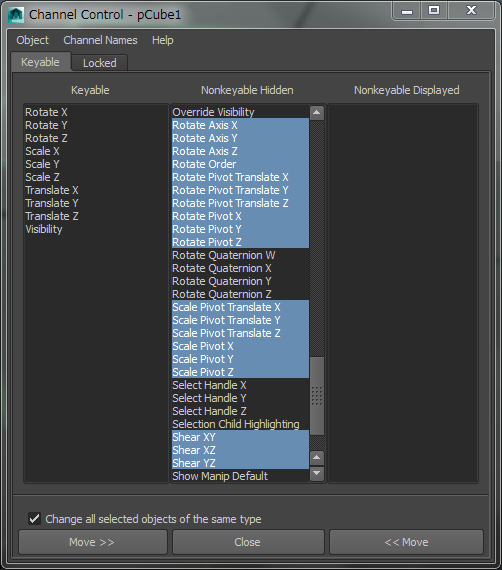
これを確認するために、以下のように Channel Box にこのアトリビュートを表示して、いろいろ試してみましょう。
ついでに座標変換にかかわる他のアトリビュートも表示しておくといろいろ実験ができます。
ちなみに、Channel Box から値を設定すると、他の値が自動で設定されるようなことはありません。

何か Transform （オブジェクト）を原点に１つ作成し、それをセレクトしたまま、 Maya のメニューバー > Window > General Editor > Channnel Control を開いて、Keyable タブで以下のとおりに アトリビュートを選択し、右下の”＜＜Move” ボタンを押します。すると Channel Box に先程のアトリビュートが 表示されます。　右側の Channel Box で選択しているのが、「裏アトリビュート」※です。 ※「裏アトリビュート」は私が勝手にそう呼んでいるだけで、一般的でも公式でもありません（笑 実験する場合、Attribute Editor か Channel Box どちらかを Maya のメインウィンドウから切り離して、 両方を表示させた状態にすると確認がしやすいと思います。

上記の状態で、（Channel Box ではなく）Attribute Editor から Pivot の値を設定して結果を確認してみてください。
これらの「裏」の値は普通は見えていませんから、Maya での作業で、ここに値が設定されていることを忘れると、
いつのまにか想定外のことになっていたりすることもあります（どんなことが起こるかは、想像してみてください）。
これは便利なようで、場合によってはちょっと迷惑な仕様かもしれません・・。

＊　＊　＊

さて、話を戻しましょう。
Rotate も Scale も Shear も、解説で組んだマトリックス単独では変換時点での座標系の原点を基準とした変換しかできません。
Pivot は これらの計算の基準を、原点から任意の位置に変更するためのものですが、
これは、移動の計算の行程を2つ加えることで実現できます。

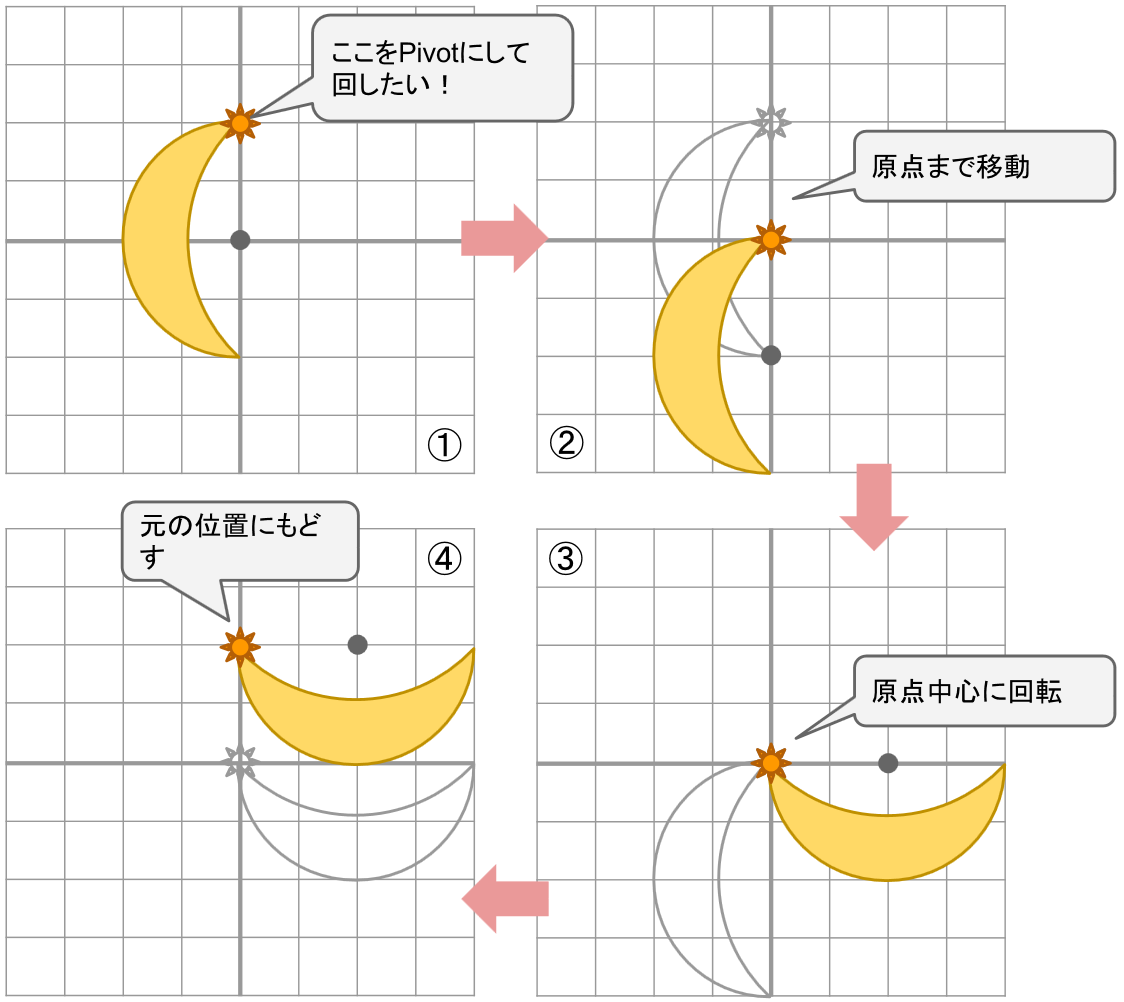
Pivot 位置を変更した場合の計算方法はこんな感じです。

1. 　Pivot の値 (x,y,z) を決める。
2. 　その値の「逆」のベクトル値分の移動を行う。
3. 　原点で Rotate などを実行。
4. 　2で移動した分を元にもどすため、Pivot の値のベクトル分移動する。

（下の図はRotateの場合）。

つまり、Rotate などの変換は原点基準でしか計算できないので、いったん Pivot 位置が原点に一致するように対象を移動して、
変換を実行したのちに元にもどすというわけです。

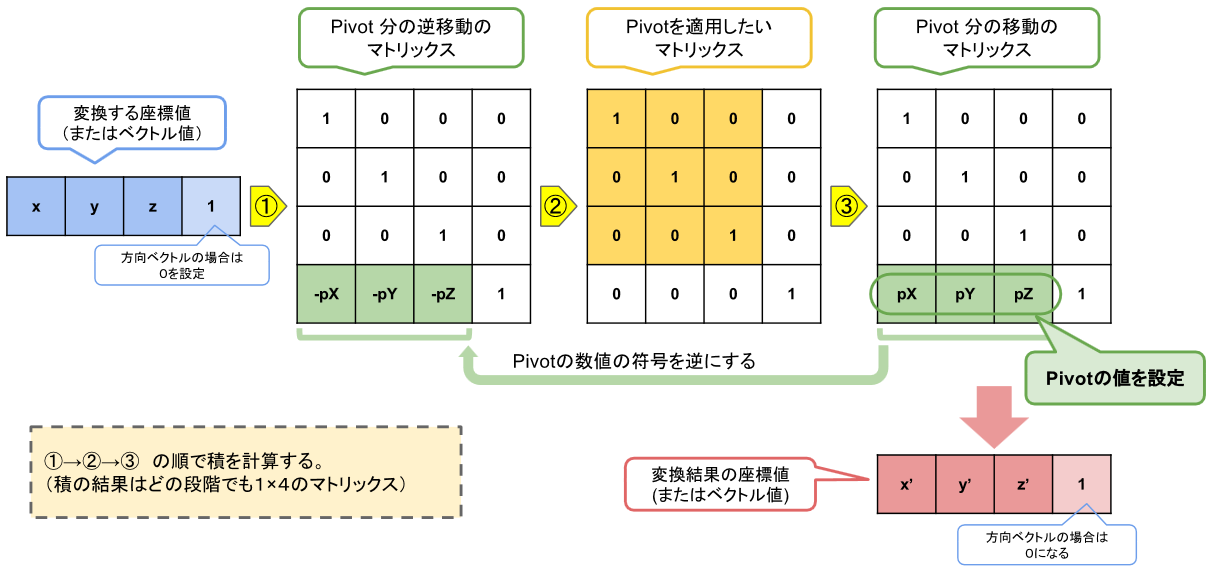
各変換への Pivot 設定の適用は、次の図のように、Pivot 値から作成する ２つのマトリックスでサンドすれば OK です。
Pivot のマトリックスの組み方は、２つのうち片方のマトリックスの要素の符号を反転する以外は、Translate の時と同じです。
※下の図では、左から右へ、マトリックスの積により段階を踏んで座標値を変換していますが、普通の処理では
先に 4×4 マトリックスを合成して１つにしてしまいます。　計算結果は同じです。

目的の変換（オレンジ色）の前後のマトリックスは互いに打ち消し合う値が設定されますから、変換のパラメーターが
デフォルト値（ Rotate 0 0 0、Scale 1 1 1　など）なら、何の変換も行わないのと同じです。

さて、ここまで長かったですが、これでひととおり Transform の個々の要素の基本的な説明が終わったようです。
rotateAxis や、Joint の jointOrient、(scale/rotate)PivotTranslate　などきちんと説明していないものもありますが、
用途は違っても、それぞれ Rotate や Translate と計算方法は同じです。今回以降の解説で出てくると思います。

そろそろマトリックスの合成の話に移りましょう。

【 マトリックスの合成 】

4×4 変換マトリックスは連結して１つに合成することができ、前もってそうすることで座標変換を効率的に行うことができます
（第一回で解説しています）。
座標変換と同じく、この合成もマトリックス同士の積を求めていくのですが、その原理と計算方法を説明していきます。

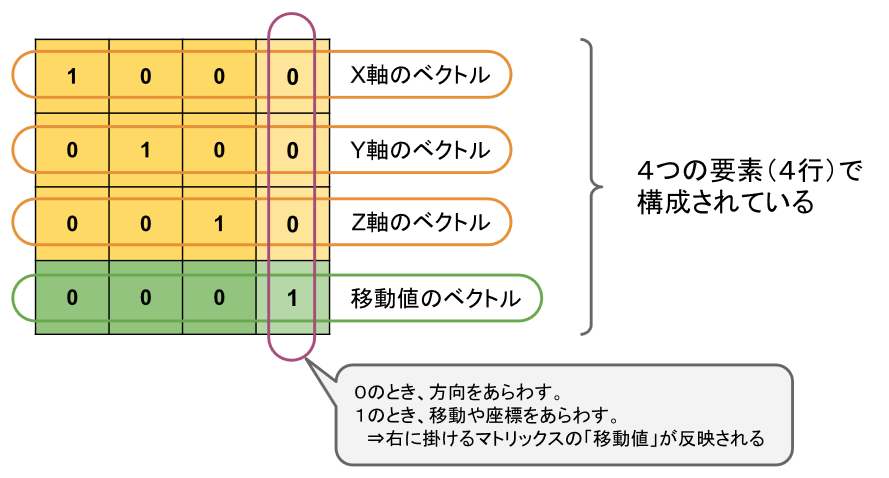
まず、前回組み立てた Translate を含んだ 4×4 のマトリックスを振り返ってみましょう。

これは３つの座標軸ベクトルと、１つの移動ベクトルの合計４つのベクトルから生成されたものでした。
これら１つ１つは、１番右の要素（0か1）を一緒に扱えば、変換対象の座標値から作成した 1×4 マトリックスと
全く同じ構成になっています（一番右の要素が 0 ならば方向ベクトル、1 ならば移動値や座標値として扱えることは
前回で少し触れましたが、それとも合致します）。
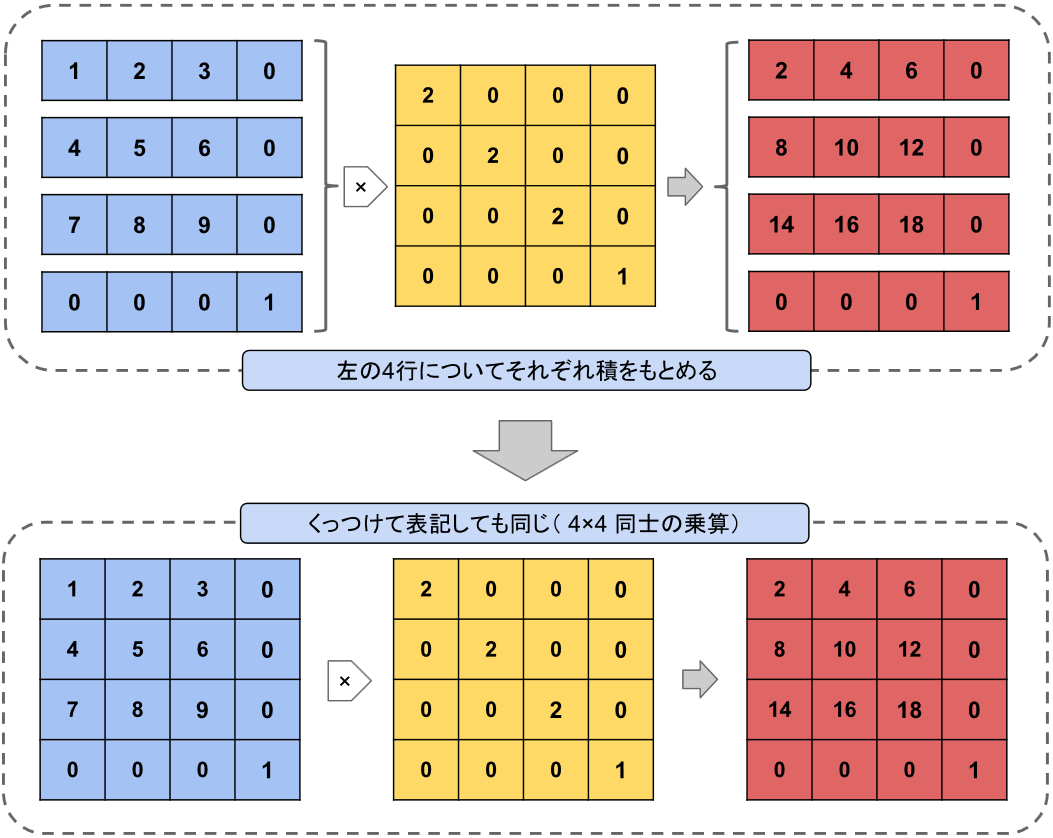
つまり、4×4 変換マトリックスの４つの各行は、座標値のマトリックスと同じように扱うこともできるということです。

したがって、これらの「行」の要素それぞれについて、別の 4×4 変換マトリックスとの積を求め、その結果から
4×4 マトリックスを再構成することで、新しい座標系を定義したマトリックスを作ることができます。
実はこれが、２つの 4×4 マトリックスを合成するということにあたります。

上の図のように、変換マトリックスの合成は 4×4 同士の積を求めるのですが、1×4 と 4×4 の積を４回計算するのと
同じなので、とくに難しいことはありません。
ただ、計算の要素数が多くなってきたので、その点ではかなり面倒になってきましたね・・・。

といったところで、今回はこのへんでおしまいです。
次回は、Maya でのオペレーションも交えて解説していこうかと思います。

※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください