わかった気になるマトリックス 第2回
2013/9/30
みなさんこんにちは。TDの土屋です。
マトリックスのお話、第2回です。前回の続きになりますので、前回をご覧になっていない方は、
を見ていただけるとすんなり入っていけるのではないかと思います。
・・・というか、見てないとわからないと思いますので、ぜひ見ておいてください!
ついでに「いいね!」等もお願いします!(笑
さて、前回は3×3のマトリックスの要素を設定し、座標変換してみるところまでを解説しました。
具体的には、各座標軸のスケールと、90度の回転のみを例として話をすすめました。
変換マトリックスは、スケール、回転、シアー、移動などのマトリックスをそれぞれに作成し、
最後に合体して1つにします。
その中でスケールは、前回の解説で理解できたのではないでしょうか。
しかし回転については90 回転の例にとどまり、まだ説明しきれていません。
もちろん、回転は任意の角度で行える必要があります。ちょっと解説が大変ですが、まずこれをかたづけてしまいましょう。
シアー(shear)についても説明したいのですが、一般的に使用頻度は少ないと思いますので、いったん後回しです。
それよりも、平行移動(translate)のほうが重要なので、今回はその解説もします。
※今回、マトリックスの合成の解説もする予定でしたが、次回にまわします。
【回転のマトリックスを定義する!】
回転のマトリックスの定義において避けては通れないものとして、皆さんが嫌いな(?)「三角関数」の知識が必要です。
ここでは解説に最低限必要なことだけを解説します。
三角関数には基本の3関数、sine(サイン)、cosine(コサイン)、tangent(タンジェント)があり、
数式やプログラムで扱う際にはそれぞれ sin、cos、tan と書きますね。
今回必要なのは sin と cos ですが、次の2次元座標での図を理解できればとりあえずOKです。
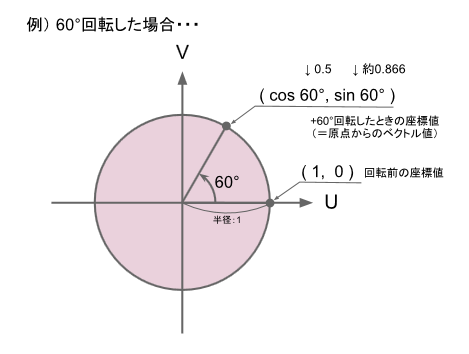
説明の都合で、図の横軸、縦軸はそれぞれU軸、V軸としています。
|
つまり、U軸上の点(Uの値: 1 )を原点中心に、任意の角度で回した座標の位置を
cos(:U方向の値) と sin(:V方向の値) を使うことで得られるわけですね。
仮に角度を60° とすれば、U軸上の点(1, 0) の回転後の座標値を得る式は、
u=cos 60° v=sin 60°
となります。
|
Maya のコマンドラインに、「cosd 60」または 「sind 60」と打って(’d’をつけるのがミソ)、 Enterを入力すると、実際の値が表示されると思います。 やってみると、それぞれ 0.5 と 0.866025 になります。 もちろん 60 を別の数値にして、どんな角度の値でも得る事ができます。 |
では、三角関数を「(一応)わかった気」になってもらったところで、変換マトリックスの話に入ります。
そもそも、変換マトリックスを定義するというのは、新しい座標軸ベクトルの値を、マトリックスの要素に組み込むことでした。
忘れかけていたら、前回の記事を見直してみてください。
ところで、Maya のTransform の回転のパラメーターは、rotateX、rotateY、rotateZ の3つがあります。
これらはX軸、Y軸、Z軸を中心に回転させるためのものですが、それぞれ、Y-Z、Z-X、X-Y 平面上での回転です。
つまり1つ1つは2次元の処理といっていいでしょう。
先程の三角関数の図も、U-V の 2次元です。これを例えば、 X-Y 平面にあてはめてれば、Z軸の回転の式として使用できます。
この式を使って回転のマトリックスを定義してみましょう。
ここで前回の記事で見覚えのある図を持ってきます。
ただし、枠内の数値は0と1だけです(色が赤いところは、これから解説する部分)。
このマトリックスは、「何もしないマトリックス」です。
どんな座標値を変換(積を計算)しても、結果は元と同じ座標値になります。
これに変更を加えることにより、回転のマトリックスを作ります。
|
※以降、変換マトリックスに組み込むこの3つのベクトルをそれぞれ、 「Xベクトル」、「Yベクトル」、「Zベクトル」と呼ぶことにします。 |
ここから、まずはX-Y平面上の回転、つまりZ軸での回転に注目して解説をすすめます。
X-Y平面上で回すマトリックスにするには、この平面を定義しているXベクトル、Yベクトル、2つのベクトルを
同じ平面上で同じだけ回転し、方向を変更します(Zベクトルには何もしません)。
X-Y平面上での回転は、Z軸での回転ですから、回転してもベクトルのZ成分の値は変化しません。
上のマトリックスの図では、XベクトルとYベクトルのZ成分は、どちらも0になっています。
ですから、これから設定するのは上の図の赤い部分のみ、つまり、2つのベクトルのX成分とY成分です。
以降、しばらくZ成分は関係ないので、ベクトルのZ成分は省略して2次元のベクトルまたは座標で説明をすすめます。
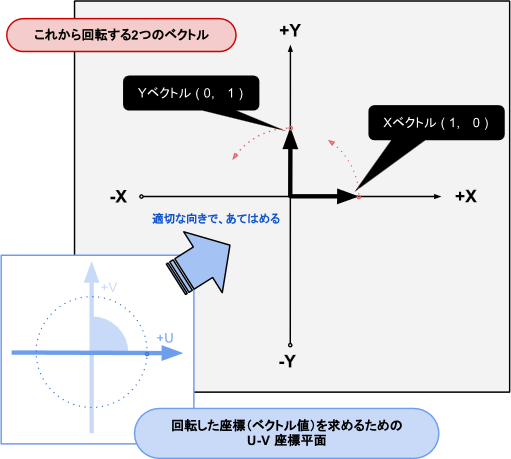
ここから2つのベクトルの回転について詳しく解説していきますが、概要は以下のようになります。
【XベクトルとYベクトルそれぞれに対して、次のように処理します】
・ X-Y平面上の回転したいベクトルに、先程のU-V回転図をあてはめる(ベクトルに 回転図のU 方向をあわせる)。
・ U-V 上で回転の計算をし、(u,v) の座標値(ベクトル値)を得る。
・ X-Y平面に投影して、回転後の(x,y) のベクトル値を得る。
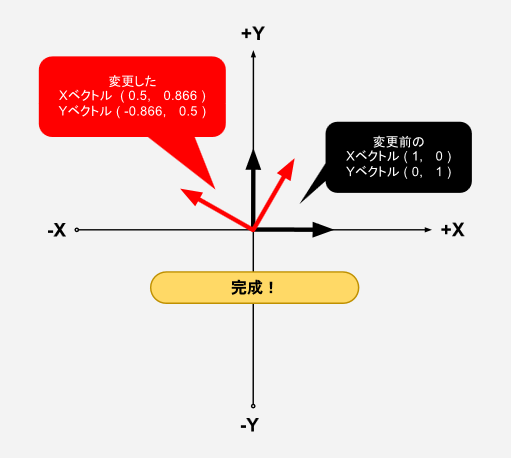
図を使って具体的に見ていきましょう。まず、回転前の状態を確認します。
例として、60°回転させたXベクトルとYベクトルを求めることにします。
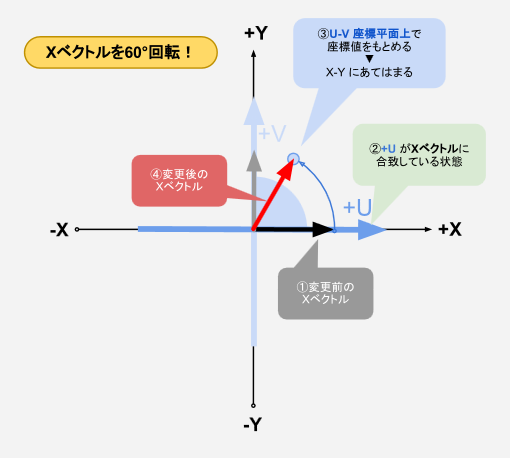
まず、Xベクトルです。初期位置としてU軸とXベクトルの方向が同じになるように図を重ねる必要があります。
ですが、この場合最初から方向が同じなので、そのまま重ねればOKですね。
回転前のXベクトルの値は(1,0)なので、回転の図のU軸上の値(1,0)と同じです。
つまり、u,v はそれぞれ x,y に置き換えることができます。
u=cos 60° v=sin 60°
なので、そのままx、yに置き換えると、
x=cos 60° y=sin 60° ※ 【Xベクトルの x と y の要素】
となります。
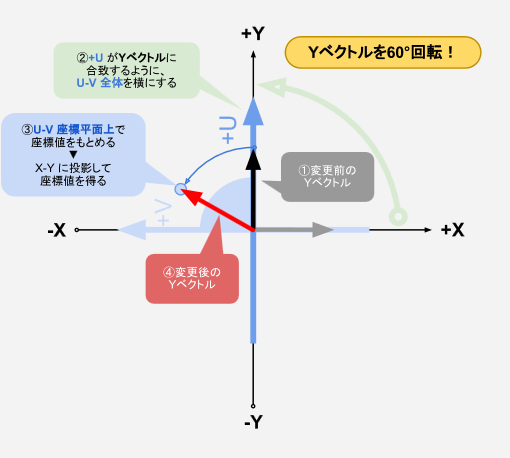
Yべクトルのほうはというと、こちらはひと工夫必要です。
U-V の図においては、最初、YベクトルはU軸上になければいけません。
U-V の図のほうを反時計に90度回転させ、U軸をYベクトルに合致させます。
u,v の式は、回す角度はXベクトルの時と同じにするので、式も同じです。
u=cos 60° v=sin 60°
これを、x と y にあてはめられるか見てみます。
まず、縦の軸に注目します。Y軸 は U軸と方向が同じなので、式の値をそのまま使えます。
一方、X軸 のほうはV軸に対応させたいのですが、XとVは軸の向きが反対です。
この場合は、式の符号を反転すれば期待した値を得ることができます。V軸の(+)の値は、X軸では(−)となるからです。
y=cos 60° x= (-1)× sin 60° ←※ uをyに置き換え。 vをxに置き換え符号を反転。
ちょっと整理して、
x= -sin 60° y= cos 60° ※ 【Yベクトルの x と y の要素】
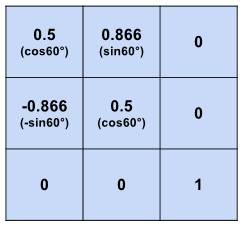
結果をまとめると、こうなります(sin 60° は約 0.866 、cos 60° は0.5 です)。
2つの軸の回転の結果、Z軸回転60° のマトリックスは以下のようになります。
ここまでのZ軸の回転と同様の方法で、X軸回転、Y軸回転についても、それぞれのマトリックスを定義できます。
X軸回転ではYベクトルとZベクトルの変更、Y軸回転ではZベクトルとXベクトルの変更が必要です。
どの場合も、U-V の図をあてはめる際には、各回転軸の+方向から見た回転平面に対して行います。
↓下の図に3つのマトリックスをまとめてみました(角度パラメーターは省略しています)。
ここで1つ思い出していただきたいのですが、transform には、rotateOrder というアトリビュートがありました。
このアトリビュートにより、上の3つのマトリックスを適用する順番を指定できます。
この順番でマトリックスを合成すると、3軸分の回転を1つのマトリックスにまとめることができます。
ただ、マトリックスの合成の解説は次回の予定ですので、詳しくは次回とさせていただきます。
【移動のマトリックスを定義する!】
3×3マトリックスでそれぞれの座標軸の「方向」は定義できました。
前回の解説で述べたとおり、回転、スケール、シアーまでは、各マトリックスを合成することで、
1つの3×3マトリックスで表現することができます。
ただ、このままだと、「平行移動( translate )」を定義する余地はどこにもありません。
しかし、変換マトリックスを拡張することで、「移動」のデータを定義することが可能になります。
1つのマトリックスに、各3軸のベクトルと、移動値を同時に定義できるようになります。
さて、ある座標値を平行移動するための計算方法は、座標値に平行移動分のベクトルを足すだけです。
(新しい座標値) = (移動前の座標値) + (平行移動分のベクトル)
ここで、ちょっと言葉を置き変えて、次のようにします。
(変換後の座標値) = (軸ベクトルで変換した座標値) + (平行移動分のベクトル)
「軸ベクトルで変換」というのは、回転、スケール、シアーで行う座標変換のことです。
前回の記事で、(3、5、7)の座標値を座標軸のベクトルを使って表すには、以下のようにしました。
(座標値)=3×(Xのベクトル) + 5×(Yのベクトル) + 7×(Zのベクトル)
そして、これらのベクトルの成分を変更することで、回転、スケール、シアーの座標変換を行うことが可能でした。
つまり、『座標値』=『軸ベクトルで変換した座標値』です。上の2つの式をまとめてみると、以下のようになります。
(変換後の座標値)=3×(Xのベクトル) + 5×(Yのベクトル) + 7×(Zのベクトル) + 1×(平行移動分のベクトル)
最後の項の「1×」は解説の都合で加えています。
意味付けすれば「平行移動分をそのまま生かす」ということを表します。
結果的に、式は、座標軸として定義した3つのベクトルに、移動値用にもう1つのベクトルを追加した形になりました。
上の式をもとに、前回の3×3マトリックスの変換の図を拡張します。
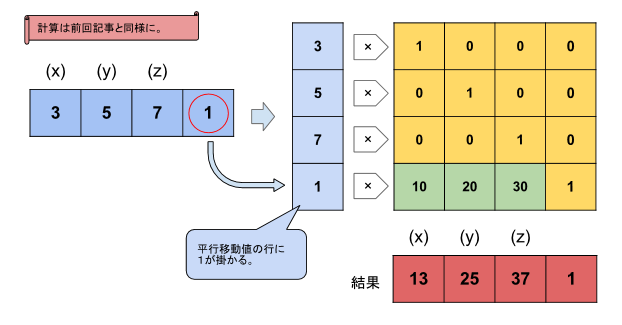
座標定義用と変換用の2つのマトリックスを下図のように定義しなおします。
座標軸ベクトルは初期値、平行移動値は(10,20,30)の場合です。
※どちらもマトリックスの右側の1列が増えていますが、↓の『右の1列をさりげなく増やしている理由』で解説しています。
|
ここでは、座標値を変換する目的なので、上の式の「1×」(=上図の赤丸の「1」)によって、「平行移動分」を 有効にしますが、変換したいのが座標値ではなく方向ベクトルの場合があとで出てきます。 この場合に「平行移動分」が反映されて方向ベクトルの向きが変わっては困ります。 そうならないようにするには、1のところに0を設定します。 平行移動分に0が掛かるので、これにより影響を無効にできます。 |
■右の1列をさりげなく増やしている理由■
縦が4になったので、横も4にしたほうが何となく良さそう・・・。
実際のところ、これは正解なのですが、ちょっと考察してみましょう。
前回、1×3の座標マトリックスと、3×3変換マトリックスの積の場合に、変換マトリックスが縦横同じ個数の正方なので、
入力座標マトリックスと出力座標マトリックスの横幅(列の数)が同じ3になりました。
今回、変換マトリックスを4×4にしたので、出力座標マトリックスの幅は、変換前と同じ4になります。
これはそのまま、再度別の4×4のマトリックスで変換することができるので、扱いやすいですね。
これが正方でないと、入力と出力でマトリックスの横幅が異なってしまいます。プログラムで処理する場合には手順が
少々煩雑になり、処理効率が低下するかもしれません。
また、正方用にしか定義されていないマトリックスの計算処理の手法なども存在します。
Mayaやほとんどのソフトで3Dの座標変換に使用されているのも、この4×4の型で、一般的なものです。
|
上図の4×4マトリックスの右下の「1」は、変換前の座標マトリックスに設定した右端の「1」を、変換後も同じく 「1」で出力するのに必要です。 座標変換マトリックスの右1列は計算上は必要のない場合もありますが、正方の形を定型とすることによる利便性を 優先しています。 0や1は、特別に計算コストのかからない値として、自動的に効率よく処理されている筈です(未確認)。 |
思ったより、回転のところの解説が多くなってしまったので、前回組んだ連載の予定とは違いますが、
今回はここまでです。アバウトな連載でスミマセン・・。
全3回の予定でしたが、4回(もしくは5回・・)になってしまうかもしれません。
・・・よろしければもう少しお付き合いください。
ではまた次回!
※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください



[…] /a> 「わかった気になるマトリックス 第2回」 […]
Posted at 2014.07.30 14:48 by デジタル・フロンティア-Digital Frontier | DF TALK | わかった気になるマトリックス 第4回
[…] 「わかった気になるマトリックス」(第1回) 「わかった気になるマトリックス 第2回」 […]
Posted at 2014.08.28 19:14 by デジタル・フロンティア-Digital Frontier | DF TALK | わかった気になるマトリックス 第3回