わかった気になるマトリックス 第4回
2014/7/29
こんにちは。TD の土屋です。
「わかった気になるマトリックス」も今回で4回目になります。早いもので第1回からもう1年が経ちました。
第1回のときに、第2回以降の記事内容の予定もそれらしく書いてみたものの、内容はぼんやりと考えていた程度
だったので、結果は予定とは少々異なった内容の記事になってしまいました。
・・そして、今回もその延長といったところです。よろしければおつきあいください。
「わかった気になるマトリックス」(第1回)
「わかった気になるマトリックス 第2回」
「わかった気になるマトリックス 第3回」
前回までの記事で、パラメータを使用してのマトリックスの組み方、変換やマトリックス同士の積の計算方法などは
説明できました。
そろそろ Maya を使用して実践的なことをしていきたいのですが、まだ少し説明しなければならないことが残っています。
Transform ノード内のマトリックス計算
第一回でも触れましたが、ここで Maya の Transform ノードを改めて見ていきます。
Mayaのマニュアルの Transform ノードの項目を見ると、最初のほうに “matrix=” の式が書いてあります
(Maya>Help>Node and Attribute Reference>Transform)。
これは、Transform が各パラメータから生成するローカルなマトリックスの式です。
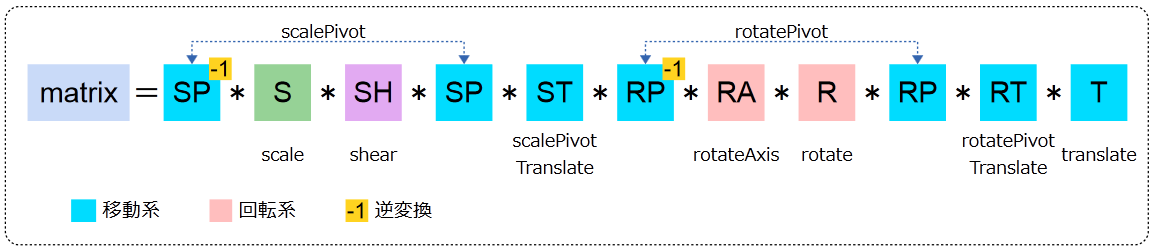
これを図にしてみました。各変換の順番を確認してみてください。
今まで解説してきた変換の要素が並んでいます。変換の種類で色分けしています。
pivot のところも理解できるはずです。「逆変換」もなんとなくわかると思いますが、下でも解説します。
マトリックスによる変換と逆変換
マトリックス化した座標値や変換値を、別のマトリックスで変換する方法は前回までの記事で説明しました。
それを用いてマトリックスによる座標変換を組み合わせた処理を考えていくと、いろいろな場面で「逆変換」を行う必要が
出てきます。
逆変換というのは、ある対象「A」を変換して「B」を得ることに対して、逆に「B」から「A」を得るための変換です。
これは、たとえば、X方向に「+10移動」の逆なら「-10移動」、スケールが「2倍」の逆は「0.5倍」といったように、
変換された対象を元の状態に戻す効果があるものです。
逆変換を行うための方法の1つとして、このように逆の状態をあらわすパラメータ値を使ってマトリックスを定義し、
それを変換の対象に適用(:積を計算)する方法が考えられます。
先ほどの matrix の図、および前回記事の Pivot の解説を振り返ってもらうと、対象の変換マトリックスを Pivot の値から
組んだ2つのマトリックスで挟むかたちになっています。これら2つのマトリックスもお互いに逆変換の関係です。
以上のように、変換のパラメータ値から逆変換を定義するのは簡単そうです。
次の表に、各種の変換に用いるパラメータを、逆変換のパラメータに変更する方法をまとめました。
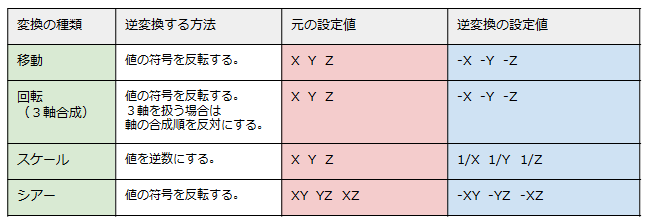
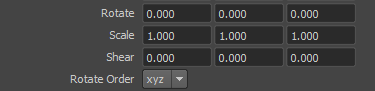
Transform ノードでは、どの変換についても3つで1組のパラメータとなっていますが、rotate だけは3軸の
処理順序の設定(rotateOrder)が影響してきます。逆変換を考えるときはこれを考慮する必要があります。
連続した変換に対する逆変換
ここで、複数の変換を連続して行っている場合に対して、その逆変換の定義はどうなるかを見てみます。
ちょうど rotate の説明をしたので、これを例にして解説してみます。
rotate は X・Y・Z 3軸に対する回転角のパラメーターから成りますが、これは3軸用の別々の変換が結合(合成)
されているものと考えてください。
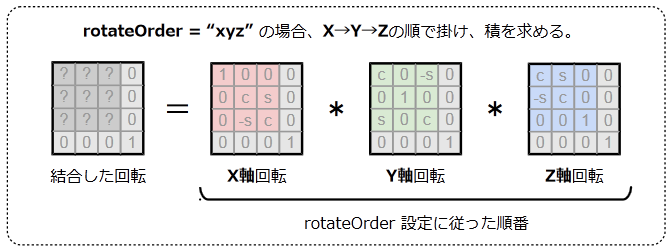
これら3つの変換は、rotateOrder により結合の順番を変えることができます。
初期状態(rotateOrder が ”xyz” )では、X→Y→Z の順番ですね。
たとえば、以下のように回転させる場合を考えてみます。
X軸で+10° → Y軸で+20° → Z軸で+30°
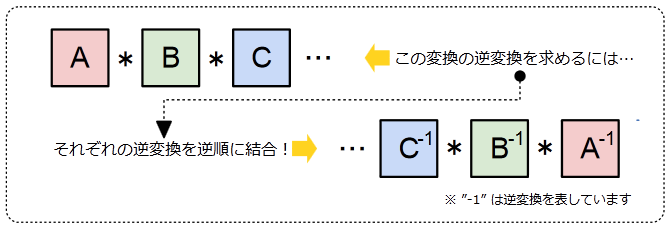
元に戻すような変換、すなわち逆変換を考えるなら、これと逆のことを行う必要があるので、
Z軸で-30° → Y軸で-20° → X軸で-10°
となりますね。変換する軸の順番は逆にし、数値の符号は全て反転させます。
上記3つの行程をマトリックスで定義して順番に積を計算していけば、3軸分の回転の逆変換マトリックスが得られます。
先ほどの例は、3軸の回転の逆変換を考えましたが、同じ考え方で、translate や scale などの変換が連続する場合も、
それらの変換を後ろ側から辿って、それぞれの逆変換を定義していけばよいです。
scale 1 2 3 → translate 10 15 20
であれば、
translate -10 -15 -20 → scale 1 0.5 0.33333
となるのですが、3つのパラメーターを分離して考える必要があるのは rotate だけで、それ以外はパラメーターの順番は
関係ないので、上のように3つまとめて扱って大丈夫です。
そして、各逆変換が決まれば、それらを合成して1つのマトリックスにすることも可能です。
|
当然ながら、rotate の3つのパラメーターの順序以外は、Transform ノード内の各要素の適用の順序は変えられないので、 1つのTransformノードに、各要素の逆変換を設定して、合成した逆変換を得ることはできません。 |
・・ちょっと説明が長くなりましたが、以上、逆変換の考え方の一つとして理解しておくと役に立つことがあると思います。
逆マトリックスを直接求める
ところで、上の方法は変換の各要素のパラメータが最初にあり、それからマトリックスを合成する場合は使えるのですが、
時には既存の任意のマトリックスから直接、逆マトリックスを得たい場合もあります。
この処理は手順が少々複雑で、処理コストもそれなりに必要な上、工夫しないと誤差も生じやすいものです。
このことは、逆マトリックスが簡単に求められる環境(関数ライブラリやシステム内で機能が提供されているなど)でも、
気に留めておいたほうがいいと思います。
逆マトリックスを機械的に求める手法はいくつかありますが、基本的に以下の条件を満たすようにします。
マトリックス × 逆マトリックス = 単位マトリックス※
「単位マトリックス※」という名称こそ初出ですが、前回までの解説中でも何度か出てきているものです。
これは変換の効果をもたない、初期状態のマトリックスのことです(左上から右下の斜め成分が1で、それ以外の成分は0)。
「逆マトリックス」は、「マトリックス」を打ち消す効果を持つものなので、積の結果は「単位マトリックス」になります。
まじめに逆マトリックスを求めるのは手順が多くて大変なのですが、以下は条件を限定した中での方法の1つです。
|
逆変換をもとめる場合、以下の条件が揃う場合には、簡単です。
●各軸ベクトルの長さが1 これは単位マトリックス内の3軸のベクトル方向を、空間内での位置関係を崩さずに全体的に回転させた状態です。 もちろん、マトリックスは3軸分の回転が合成された状態でかまいません。 |
|
記事の都合上、上記以外の逆行列を直接求める具体的な方法の解説はこの記事では割愛します。興味のある方は、 以下のキーワードの組み合わせで web 検索してみてください: 逆行列 & ( 掃き出し法 ガウスの消去法 LU分解 ) |
合成されたマトリックスの逆変換を求める方法としては、マトリックスを shear、scale、rotate、translate 成分に
分解できれば、その上で個々についての逆変換を求めることでもなんとかなりそうですが、それもまた別の機会に・・・。
Transform ノードの階層とマトリックス
ここからは Transform ノードの階層の話です。やっとここまで来ました。。
ご存知のとおり、Transform ノード同士は、親子関係を定義し、階層化することができます。
子は親の変換を引き継ぎ、さらに孫へと変換を引き継ぐことになります。
Transform のパラメータは、その Transform のローカル空間でのマトリックスを定義します。
それを使用すればローカル空間内の変換は可能ですが、仮に結果が座標値ならば、多くの場合、最終的にはワールド空間への
変換が必要です。ワールド空間への変換を行うためには、あるTransformノードの親と、その祖先にあたる全ての階層の情報が
反映されたマトリックスを得る必要があります。
実際には、ある Transform における、ワールド座標系へのマトリックスを得るのは簡単です。次のようにします。
(ワールドのマトリックス) = (ローカルのマトリックス) × (1つ親のワールドのマトリックス)
親のワールドのマトリックスがわかっていれば、自身のワールドもすぐ得られます。
親がいなければ(root なら)、「ワールド=ローカル」となるだけです。
実は、各 Transform ノードは、自身のローカルのマトリックスとともに、ワールドのマトリックスも計算してアトリビュートに
出力する仕組みになっています。
これにより、自身のワールドを計算するとともに、その子孫にもワールドを計算する情報が提供できるようになっているのです。
ここで、Transform ノードが持っている matrix タイプのアトリビュートを確認してみます。
Maya のマニュアル上では、Transform だけではなく、その親分(親クラス)にあたる dagNode というノードの解説も見ます
(Maya>Help>Node and Attribute Reference>dagNode)。
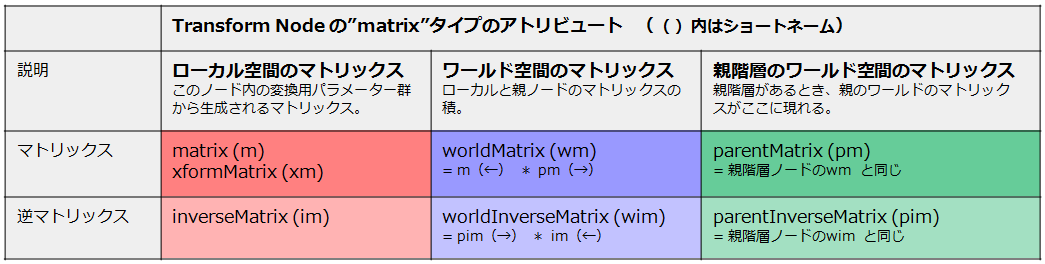
(表の中に、実際は1つで複数のマトリックスを出力するタイプのアトリビュートがありますが、ここでは気にしません。
“xformMatrix” もここでは触れません。)
・・なんだかいっぱいありますが、恐れる必要はありません。まず、中心役は自身のローカルの値が反映される”matrix”です。
今まで解説してきたのは、このアトリビュートを生成するための原理です。
逆マトリックスが出力されていますね。これを使えば、場合によってはわざわざ逆変換を求めなくてもいいかもしれません。
●名称に「inverse」を含んでいるのが3つあり、それぞれ含んでいないものに対する逆マトリックスです。
●名称の先頭に「parent」がついているものが2つあり、これは階層化した際に自身の親にあたるノードのワールド値が
見えているだけのものです。
これらマトリックス関連のアトリビュートはすべて読み取り専用で、ここに直接値を設定することはできません。Transform
ノードに設定したパラメータ(transform,rotate などの値)から、ノードによって計算されたものが出力されるのみです。
さて、これだけだとちょっとピンとこないと思いますので、以下の図を見てください。
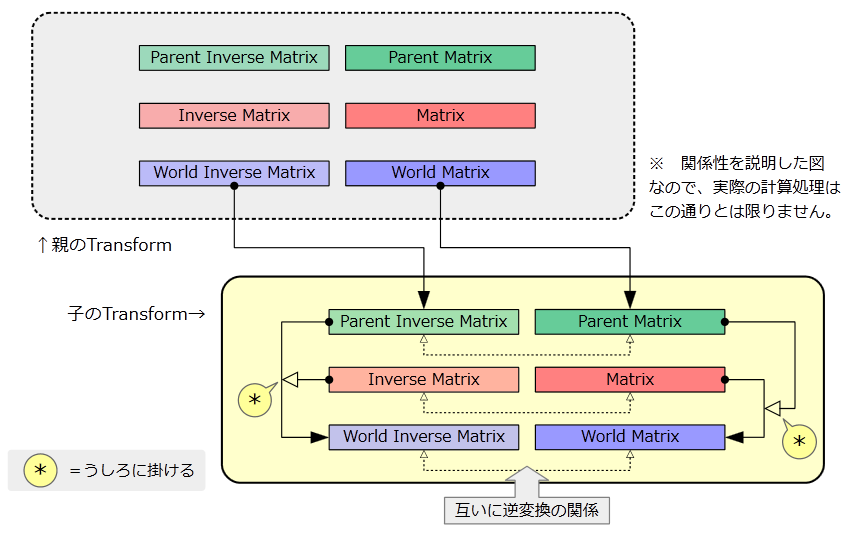
2つの Transform ノードを階層化した際の各アトリビュートの関係です。
矢印方向に情報が引き継がれていくと考えてください。”*” は積を計算するところです。
「matrix」 に注目すると、「parentMatrix」 の情報を得て、「worldMatrix」を設定している、といった感じです。
Inverse 側はちょっと違っていますが、逆変換同士の積では順番を逆にする必要があるためです。
階層における計算の順番
たくさんの Transform ノードで階層を構成している場合、どういう順番で計算されるべきでしょうか?
基本的には、階層内の各部分それぞれの「親」と「子」2つのノード間で依存関係があるので、計算の順序は自動的に
決まってくるはずですね。
たとえば、親ノードの状態が決まらないと子ノードの状態は決められません。
各階層のいくつかのパラメータがアニメーションするとして、あるフレームの状態を計算しようとする場合、現在の状態から
変化していない部分があれば、すべてのノードについて計算をする必要はないかもしれないし、そうでないかもしれません。
実際には、Constraint や IK など、階層の処理にいろいろな要素が加わってきて複雑なことになります。
Maya を使用する場合においては、これらの処理の判断は Maya にまかせることになりますね。
きっと無駄なく適切に処理してくれている、と信じるしかないです・・・(時々裏切られている気もしますが)。
「わかった気になるマトリックス」はこちらの第四回でいったん終了となります。
長らくのご愛顧、誠にありがとうございました。
※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください



コメント
コメントフォーム