ICE Kinematics でオリジナルIK(後編) -余弦定理&回転の合成 -
2011/8/22
Tag: ICE,ICE Kinematics,softimage,tips
ご無沙汰しておりました。SoftimageのTDをやらせてもらってる上原達也 です。
前回の投稿からかれこれ半年近く・・。
いろんなことが目まぐるしく変わっていきますね。DFはエキサイティングです。
今回は前回に引き続き、オリジナルIKをICE kinematics で仕込む後編をお届けします。
※前回記事へのリンク「ICE Kinematics でオリジナルIK(前編) - アップベクターと制限角度の仕込み -」
とはいえ最近ICEを触っていない&時間が経ちすぎて完全に忘れてしまいましたよっ。
ちょっとだけおさらいします。(自分のためにも)
前回のポイントが何だったかと言うと、
アップベクターとIK部分は分離して考えますよー ということと、
ある角度で制限(ロック)かけたいので事前にその角度を計算しときますよー でした。
そして、今回やるのはそのIKの核となる部分と、分離して考えたところを合体するです。
■ 【余弦定理と回転の合成】
まずはじめに、「余弦定理と回転の合成」とありますが、それぞれ何のことを言ってるのがざっくり説明。
「余弦定理」 → 各骨の角度を求めるために使います。
すべての辺の長さがわかっていれば、角度が求められたり、
2辺とその間の角度がわかっていれば、残る1つの辺の長さを求められたり。
「回転の合成」 → 余弦定理によって求めた角度と
前回の「アップベクター」の部分で求めた角度を合成することを指します。
そのときのICEの加算、乗算ノードの謎仕様などについて。
■ 【余弦定理】
「そもそも、余弦定理ってなんだっけ?」
説明はネットでいくらでも調べられるので、今回必要な情報だけ書いてみます。
「三角形において、三辺の長さが決まっていれば、すべての角度も決まる!」
かなり強引な説明ですが、わかりやすく書いてみました。(誰かに突っ込まれそう
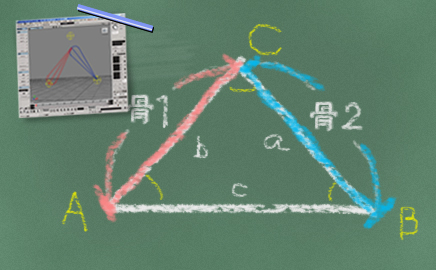
※小文字の” a , b , c ” は”辺” を意味します。
※大文字の” A , B , C “は”角度” または “角” を表しています。
三辺の長さについては、
骨1の長さ(辺b)
骨2の長さ(辺a)
骨1の根元と骨2の先端の距離(辺c)
と、すぐにわかるのでこれを使って各骨の角度を求めていきます。
スクリプトやノードで作りやすいように少し書きかえます↓
” cosA = ( b*b + c*c – a*a ) / ( 2*b*c ) ”
ただし、このままだと左辺のコサインが邪魔ですので整理します。
“A = ArcCos(( b*b + c*c – a*a ) / ( 2*b*c ))”
右辺を逆余弦関数(アークコサイン)でくくってあげることで、左辺を A (骨1の角度)だけにすることができました。
実際にノードを組むとこんな感じです。
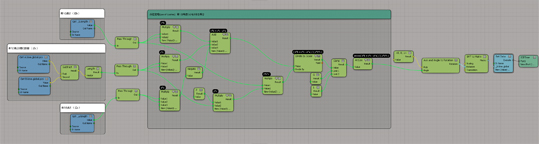
※リンク先の画像デカいです。
C(骨2の角度)も同様の方法で求めることはできるのですが、
AがわかったおかげでCは別の方法で求められるようになります。
| と、その前に気をつけなくてはいけないこと。 ICE kinematics では、元のオブジェクトが階層構造であろうが、なかろうが基本的にグローバルで値をセットします。 ということは骨2(辺a)の角度をセットするには2パターン考えられます。 1.骨1(辺b)の座標空間を元に計算したのち、グローバルに戻して値をセット。 2.直接グローバルで計算して値をセット。 |
|---|
1の方が感覚的にわかりやすそうですが、実は2の方が都合がいいのでこちらでやります。
まずは、最終的にどこの角度を求めてセットするか?。ここです↓
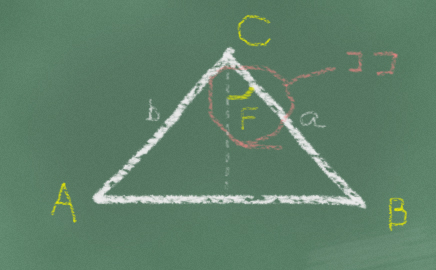
仮に角度 ” F ” とします。
この角度が骨2(辺a)のグローバルな値になります。
さらに、その角度を求めるために知りたい部分は?。ここです↓
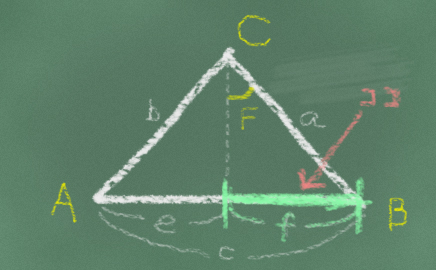
画像のように 辺 ” f ” と 辺 ” e ” とします。
ではまず、この 辺” f “ から求めてみます。
” f = c – e “ ですが、
” c “ は既に分かっています。
” e “ は ” b ” を ” c ” に投影した内積なので、ベクトルを使って長さを求められますが、今回はベクトルでやりません。
ほかの方法として、三角関数で求めることが可能です。
” cosA = e / b “ です。
” e = “ の形になるように変形します。
” e = b * cosA “
” cosA “ はもう知っていますから、上の方でやった式と差し替えて
” e = b * (( b*b + c*c – a*a ) / ( 2*b*c )) “
” cosA “ だった部分に ” b “ を掛けると、分母の ” 2*b*c” から ” b “ が消え
” e = ( b*b + c*c – a*a ) / ( 2*c ) “ になります。
今回はこれを使ってみます。
この ” e “ を求める式は、 ”cosA” を求めたときの式にかなり似ていますよね。
” cosA = ( b*b + c*c – a*a ) / ( 2*b*c ) “
↑↑↑ ほとんど一緒! ↓↓↓
” e = ( b*b + c*c – a*a ) / ( 2*c ) “
ということは、ノードの途中から値を引っ張り出せばよさそうです。
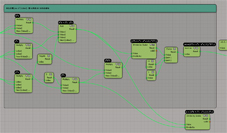
↑これで ” e ” が求められました。
というわけで ” f ” を求める式はこうなります。
” f = c – (b*b + c*c – a*a ) / ( 2*c ) “
または
” f = c – b * cosA “
では最後に 角度” F “ を求めます。

緑色のラインの三角形において、
辺” a “ と 辺” f “ の長さが分かっているわけですから
三角関数より、
” sinF = f / a “ が成り立ち、
角度” F ” = arcsin( f / a ) で求められます。
これで、骨1と骨2の角度が分かりました。
ここまでのノードはこんな感じです。
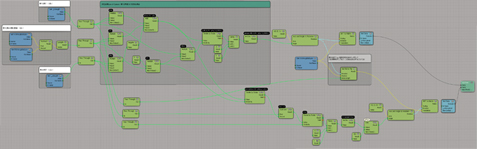
※リンク先の画像すごいデカいです。
※説明はしてませんが、画像では骨2の「ポジション」を設定するためのノードが追加してあります。
ただしこのままでは、↓このような動きのときしか考慮されていません。
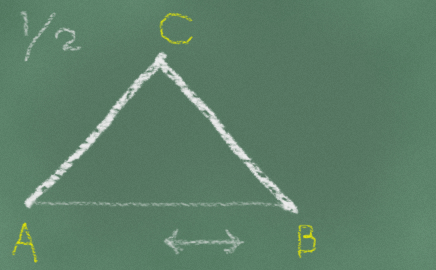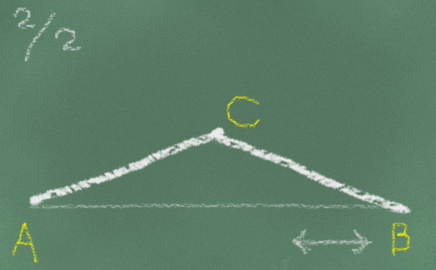
↓こうなったときの「ココ」の部分の角度は無視しています。
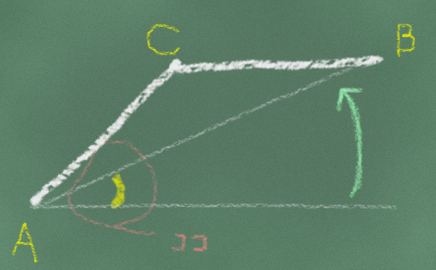
それじゃ駄目じゃないかと思われるかもしれませんが、実は問題ありません。
なぜなら、
前回の記事で説明した「方向コンストレインとアップベクターの部分」が
そこの角度を持っているからです。
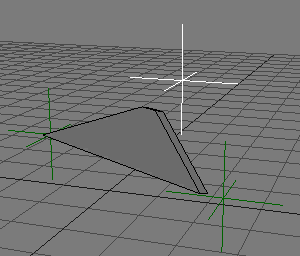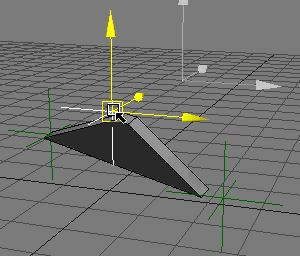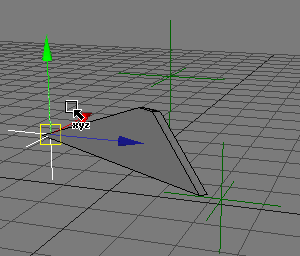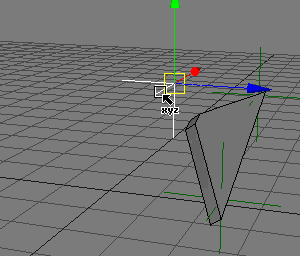
これによってIKの部分がかなり簡単に実現できたと思います。
■ 【回転の合成】
上で求めた各骨の角度と、前回の記事の「方向コンストレインとアップベクターの部分」の角度を合体させます。
どのように回転を合成させるのかですが、ヘルプに記載されてました。
|
Softimageユーザーガイド 目次 - ICEの基本 - ICEツリーの構築 - 変形の操作 - 回転の操作 ”” ・ 2つの回転(軸および角度)の値を乗算または加算する。 ・ 2つのクォータニオンを乗算する。 ・ 2つのマトリクスを乗算する。 オイラー角を表す2つの3Dベクトルを乗算しても、正しい結果を 得られないこと(および実際には幾何学的な意味を持たないこと)に注意してください。 ”” |
|---|
と、ここで気になるのは ”乗算または加算する” という部分。
どっちに繋いでもいいということなのでしょうか?
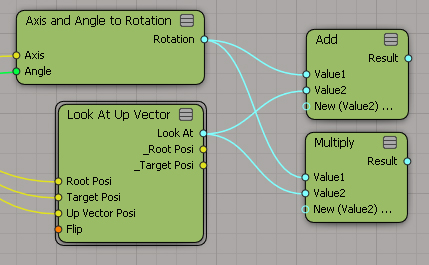
試しにこのようにノードを組んでみたところ、
加算ノード、乗算ノードともに出力された結果は同じでした。
今度は繋ぐ順番を変えてみます。
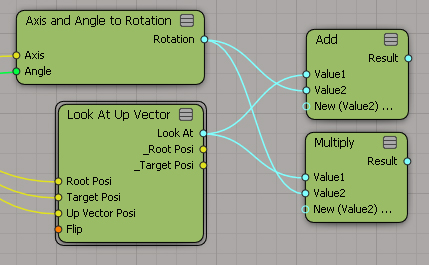
さきほどと出力される結果は違いますが、
加算ノードと乗算ノードから出力される結果が同じという点は変わりません。(え?
RotationノードはAxis-Angle(任意回転軸、角度)で定義されていますが、
乗算するときにマトリクスに変換されているようです。
このマトリクスは、乗算の交換法則が成り立たない(掛ける順番によって結果が違う)ため、
画像のように繋ぐ順番をかえて、乗算ノードの出力結果が変わるのは正しいです。
しかし、
加算ノードも同じように出力結果が変わるんです。
なんて気持ち悪いことでしょうね。
※ちなみに明示的にマトリクスに変換して、加算ノードに繋いだ場合、マトリクスの各成分が単純に足されるだけなので、繋ぐ順番によって結果が変わるなんてことはありません。
どうやら、Rotationが加算ノードに直接繋がっている場合、
マトリクスで乗算ノードに繋いだ状態と同じものになってしまうようです。
なんだかスーパーウルトラスペシャルややこしいですね!
※ただ、ちょっと自信なかったりもします・・・。この辺のこと知ってる方いらっしゃいましたら教えてください(泣)
※ちょっと補足 - ICEの算術系ノードは繋がれたノードのタイプによって七変化します。どういうことかといいますと、クォータニオンが繋がっているときはクォータニオン用の計算、マトリクスが繋がっているときはマトリクス用の計算を自動してしてくれるというものです。ただ、タイプの違うもの同士を直接繋いだりはできませんので、その場合は別途変換ノードを噛まして接続したりします。
というわけで、どっち使ってもいいみたいですが、
気持ち悪いので加算ノードは使わず、乗算ノードを使ってICETreeを組んでみました。
余談ですが、FKとIKのブレンド機能を実装しようと思ったら、乗算する前にクオータニオンに変換しておいた方が球面補間とか使えるので幸せになれそうな気がします。
完成ムービー
■今回の記事で取り扱った内容のサンプルシーン■
ik_sample.zip
■ 「最後に」
今回説明できませんでしたが、あとは前回の記事で求めた制限角度を使って「角度が制限角度に達したらロックする~」というような
条件分岐のノードを組んであげれば、角度制限付きIKの出来上がりです。
■角度制限まで組んであるサンプルシーン■
DF_LimitAngleIK_v2.0_SI2011.5.zip
前回から今回までのこれらの作例は試作的な意味が大きかったので最適化・高速化されてませんから、
実際使うの場合はいい感じにカスタマイズする必要があるかと思いますのでご注意ください。
最後までご覧くださってありがとうございました。何かしら皆様のお役に立てれば幸いです。
また、何か追加で説明が必要なことがありましたらコメント等いただけるとうれしいです![]()
※注意※ 本記事内でダウンロード可能なサンプルシーンを使用したことによって引き起こるいかなる損害も
当方は一切責任を負いかねます。自己責任でご使用くださいませ。


コメント
コメントフォーム