Projective Dynamics

2017/2/20

Tag: math,projective dynamics,simulation

皆さん、こんにちは。
開発室のVladimirと申します。
前回約束した通り、今回はProjective Dynamicsについてお話させていただきたいと思います。

相変わらず、Simulationについて数学的な視点で話をしたいと思います。この記事の対象者は開発者としてSimulationに少し経験と知識を持ち、Projective Dynamicsに関してほとんど知らない人です。すなわち、Finite Differences, Explicit/Implicit Eulerなどの定義が分かる人です。実装ができるようになるため、この記事は少しでも役に立てば幸いです。

私は少しずつ知識を得ているので完璧に理解しているとはいえませんが、「何を実装するか」「何を応用するか」という決断するのが必要な時に重要な情報をここでまとめました。数式の証明などを省略させていただきますが、Projective Dynamicsの理論的なdiscussionはコチラで勉強できます。

※そのチャネルはProjective Dynamicsを考案した一人のチャンネルなのでCG研究についてのビデオはたくさんあります。お勧めです。

略語

1. Projective Dynamics: PD
2. Position Based Dynamics: PBD
3. Block Coordinate Descent: BCD
4. Finite Elements Method: FEM

Projective Dynamics(PD)とは

一言でいえば物理システムのdynamics式を解く方法です。

Dynamics式は物理の外力、内力とinertiaの影響を考慮しながら時間軸に対して粒子の挙動を求める式です。時間軸を分離するためにImplicit Euler法を応用すれば、式はこのようになります:

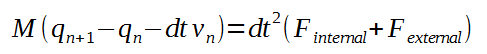
1. Mは粒子の質量
2. qは粒子の位置
3. dtは時間方向軸のステップサイズ
4. Fは力

立体弾性的なsimulationをする時、各粒子は近傍の粒子に繋がっていて、弾性的な内力が発生します。

Dynamics式を解くのは下の式を最小化するqを求めると同じです。

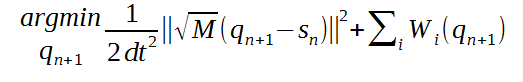
1. nはcurrent iterationです。n+1はdt時間がたってからのiterationです。
2. sはIteration nにて既に持っている情報をまとめているvectorです。つまり、外力、現在のvelocity、現在の位置情報です。
3. Wは内力を発生するenergy関数です。複数の単独energyを合わせて、total energyになります。

その式を最小化するためにどのように空間を分離するか、また、total energyをどのように定義するかを決めます。やり方はいくつかあり、PDはその一つです。

一般的にはよくNewton-Raphson method (ニュートン法)が使われます。ニュートン法は任意のenergyを対応できるので自由性と正確性が高いです。

PDはニュートン法より速くdynamics式を解く方法です。そのために制限のあるenergy関数を使うので、自由性がなくなり、他の問題もあります。

ニュートン法との比較

ニュートン法による式の解き方はネット上で教材が沢山ありますので今回は詳細を省略させていただきますが、重要なポイントをまとめておきます：

1. 各iterationをさらにsub-iterationに分解します
2. 各sub-iterationには一つの線形システムを組み合わせます (Ax=b)
3. その線形システムの解答は現在の位置情報より正確な解答に近いので、位置情報を更新します。

一方、PDは次の特徴があります：

1. 各iterationをさらにsub-iterationに分解します
2. 各sub-iterationにはbベクトルを求めます。 (行列Aは一定です)
3. その線形システムの解答は現在の位置情報より正確な解答に近いので、位置情報を更新します。

すなわち、1と3は共通ですが、2で大きく処理時間が節約でき、ニュートン法より速く結果を出すことが可能です！

但し、高速化するため、energyは制限されますのでニュートン法より多くのenergy関数の対応は不可能になります。

Energy関数

PDにての内力はpenalty forcesとして定義されています。

Penalty Forcesというのはある条件を満たしていないときにその条件を満たせるようになるための力です。

バネのような力で例えれば、伸びているsegmentは安定する長さに復元するような力があります。

total energy関数は複数の拘束条件により内力のsummingとして定義され、最小化される関数はこのようになります：

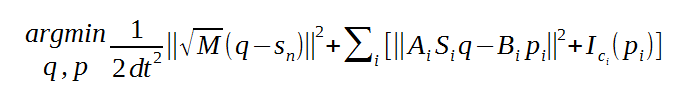
1. AとBの行列は一定です。
2. Sは選択するための行列です。つまり、qには全頂点が含まれていますが、iの拘束条件にはいくつかしか含めていないとき、その対象外の頂点をゼロに乗算します。
3. pは中間的なベクトルです。pの役割は後述します。
4. I(p)は拘束条件を満たしているかどうかをあらわしています。満たしている時にゼロで、満たしていないときにinfinityです。

そこで、inertiaとtotal energyを最小化するため、BCDが採用されています。

1. まず、現在の位置情報からスタートします。
2. qを固定して最小化します。これはLocal Stepと呼ばれています。
3. そして、pを固定してまた最小化します。これはGlobal Stepと呼ばれています。
4. 更新されたqを持って、inertiaとtotal energyの足し算は指定したエラー以下になるまで繰り返します。

関数を三つに分けるとInertia, DistanceとI(p)の部分になります。

Inertiaはpに非依存性なので、Local Stepで無視できます。

DistanceとI(p)を最小化するため、まず、I(p)の定義を見てみましょう。

もしpはその拘束条件を満たしていなければ、Distance + I(p)はinfinityになるので、関数は最小化されていなくなります。

そのため、I(p)はただ「可能な形状の中から拘束条件を満たしている形状しか使わないよ」という部分です！

それをもって、Distanceを最小化できるpは拘束条件を満たしながら、qから一番近いpを選ぶのです。

すなわち、pはqが拘束条件を満たしている形状spaceに投影(projection)されたものです。これらの事からProjective Dynamics法という名前の由来になっています。

下図で簡単なsegment length拘束を例としてご覧ください。

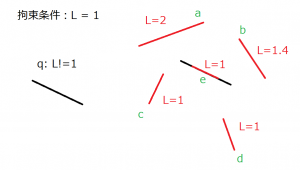
1. まず、可能な形状としてa,b,c,d,eがあります。
2. I(p)により、c,e,dを選びます。
3. 元々の形状のclosestはeです。
4. 答えはp=eになります。

次にGlobal Stepに移動します。

I(p)はqに非依存性なので、無視できます。それはPDの特徴です。

拘束条件の非線形性はI(p)に含まれるので、Global Stepで無視でき、線形的なforceだけを扱えるようになります。

最小化するために、関数の一次導関数を計算します。その結果がこちらです：

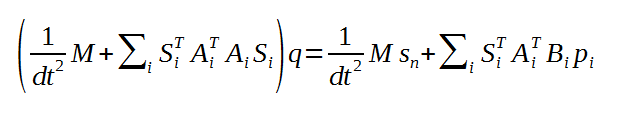
これは線形システムの形です。 (Ax=b)

左方の行列は一定になります！つまり、事前に行列を組み合わせてinverseなどを計算すればdirect法を応用できます。

ニュートン法との比較

ニュートン法はenergyに関して以下の様な特徴があります：

1. 非線形なenergy関数を対応できます。
2. 各sub-iterationには線形システムの行列が変わりますので、direct法を使わなくなります。
3. システムを求めるために、一次導関数(Force)と二次導関数(Hessian)が必要です。

一方、PDは：

1. 拘束条件として線形的なForceを発生するenergyのみを対応します。
2. 各sub-iterationではb vectorのみを求めます。
3. 行列に依存している特徴(mass,dt,topology)が変わらなければ、事前計算で必要な情報を計算できてdirect methodを応用できます。

Performance

PDのsub-iterationは明確にニュートン法より速いですが、目的はDynamics式の最小化です。

ゼロエラーの結果は無理ですが、エラーの減少率はPDとニュートン法は違います。

論文の結果をご覧ください：

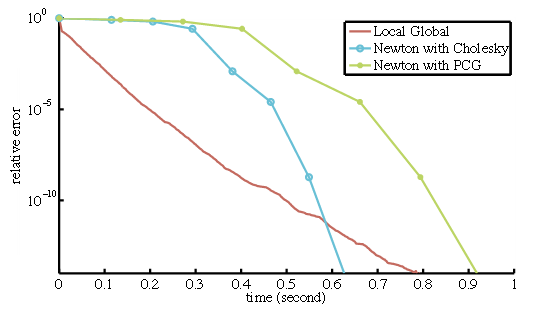
縦軸はエラー値で、横軸は時間です。

10^-11ぐらい以下のエラーが必要であればPDは負けますが、CG Simulationとしてはそのように厳しくはないです。

但し、それは論文で発表された一つの例だけです。事実の証明にならないですが任意のsimulationに対しても同じ結果がでるとおもいます。(SIGGRAPHで発表されたぐらいなら…)

PDとほぼ同じ方法はPBDがあります。アルゴリズムはほぼ同じですが、各sub-iterationで拘束条件をひとつずつ強制的に満たさせて、qを更新させます。

そのやり方はPDより遅く近似するので、PDより遅いです。

Simulation Quality

まず、非線形なenergy関数を対応しない時点で、quality的にニュートン法に負けます。

弾性的な物質をsimulationするなら、FEMやmass-spring的なenergyを使います。

それぞれは非線形なので、簡易なenergyに変えてからPDに入れ込めますが、リアル感は少しなくなります。

但し、それほど非現実ではないです！

PBDに比べると、PDは矛盾している拘束条件を対応できます。

PDはそれぞれの拘束条件とinertiaとのバランスを取るので結果は全てを100%満たさない可能性がありますがquality的にPBDより高いです。

PBDには矛盾している拘束条件があれば、ほとんど満たされていない条件が残りますので、その問題は結果に出やすいです。

Penalty Forcesを扱っている方法では、根本的にsimulationの安定さに問題があります。特にhigh stiffnessのsimulationをしている時、不自然な内力が発生しやすいです。

それに関して、私は詳しくないですがコチラでその問題を解決しているので、興味があればご参照ください。

まとめ

1. CG simulationにはPDがニュートン法より速いです。
2. PDは実装しやすく、customな拘束条件で拡張しやすいです。
3. PDは線形的なenergyしか対応できないのでultra-realisticなsimulationを目指しているなら、ニュートン法の方が良いです。
4. PDは拘束条件を100%満たせないです。
5. PDの高速化を使いこなすため、行列を事前計算し、on-memoryデータで格納するのが必要です。high-resの物体をsimulationするなら、巨大なデータ量を使います。

これでProjective Dynamicsの紹介は以上となります。説明が明確ではないところがあれば、最初の参考ビデオを是非見てください。１時間程度のビデオですが、説明はわかりやすいと思いました。他にPDとPBDの比較について詳しく書いてある記事はコチラにあります。【日本語】

※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください。