物理シミュレーションを高速化 - Accelerating Physical Simulations
2016/7/11
Tag: SIGGRAPH,simulation
お久しぶりです!
開発室のVladimirと申します。
久々に記事を書いてみましたが、今回、面白くて必ず役に立てる情報を伝えさせていただきたいと思います。
さて、はじめましょう。
簡単に線形システムの演算を高速化できる方法を紹介させていただきたいと思います。その方法はSIGRAPH ASIA 2015で発表され、こちらで公開されています。
論文のタイトルは A Chebyshev semi-iterative approach for accelerating projective and position-based dynamicsです。
方法の魅力を十分に把握する為、まずはCGにおける物理シミュレーションの基礎を理解するのが必要なので、簡単にその説明からはじめたいと思います。例としては髪の毛のシミュレーションを題材とします。
物理シミュレーションのブレイクダウン
運動学的な動きのみを扱うのであれば、シミュレーションは必要ではありません。例えば、free fall (自由落下)で動いているparticlesなら、ある瞬間に対して加速、速度、位置を持っていれば、任意の瞬間 t に対しての速度と位置を簡単に計算できます。しかし、弾性力や圧力などの現象を扱う場合、物体の位置を即決定する方程式を簡単に求めることができません。一般的な挙動を表す方程式は偏微分方程式( partial differential equation)を使います。ある変数の変化率の関係を表します。例えば、弾性シミュレーションのdynamicsは次の方程式を基づいて行われています:
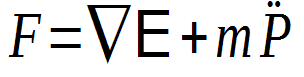
一般的に髪の毛は弾性物体としてシミュレーションされているので、ここから弾性エネルギーを例として見て行きましょう。
方程式であらわされている現象はシステムの全体エネルギーの固定性です(外力はゼロの時)。運動エネルギーの変化率と内弾性エネルギーの変化率は同じです。シミュレーションされている頂点は動き始めると、その動作をキャンセルするための弾性エネルギーが蓄積されていきます。
連続体を扱っているので、方程式の答えは単純な関数で表すことができません。正しい挙動を近似できる方法を採用するのが必要です。一番簡単でよく使われているのは 有限差分法(finite differences methods – FDM)です。
Dynamics式の分離
有限差分法にて、ドメイン(x,y,z,t)を分離して、連続微分式をサンプルした微分式に変形します。例えば、2次微分は次の式に近似されています:
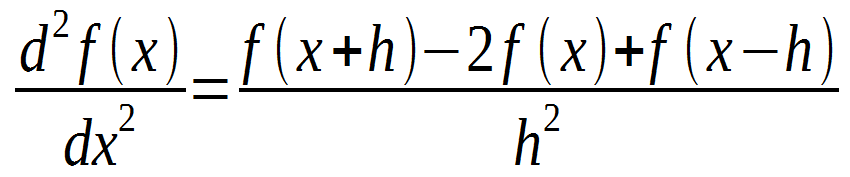
頂点 P = P(x,y,z,t) での連続微分はその位置の関数値とoffsetした位置の関数値を持って近似されています。時間軸方向に考えれば、経過時間のhを与えると、t+hでの形状はtとt-hでの形状から求められます。つまり、今と前の形状を持っていれば、次の形状をcomputeできます。
但し、近似なので【次の形状】は完璧に正しいとはいえません。timestepは小さければ小さいほど、完璧な結果に近づきますが1秒のシミュレーションをする為、必要な反復回数は増加します。マシンの精度の問題もありますので、精度とスピードのバランスを考えて最適なtimestepを探すことが重要です。
Dynamics式はもう一つの連続微分があります。弾性エネルギーの勾配 (gradient)です。こちらもFDMを使うことが可能ですが、3D空間を分離することが必要です。しかしシミュレーションされている物体はdata structureで分離されており必ずしも均一とは限りません。Hairの場合であれば髪の長さが不均一であったりするため、FDMを応用するのが困難になりますので別方法を使います。
選択肢としては、バネ質量システム (mass-spring system)と有限要素法(FEM)などがあります。それぞれの方法の詳細は割愛させていただきますが、結果的にある頂点 P = P(x,y,z,t)のエネルギーはその頂点に繋がっている頂点のみに依存しています。次の式は各頂点のエネルギーと隣接する頂点の線形的な依存性をあらわしています。
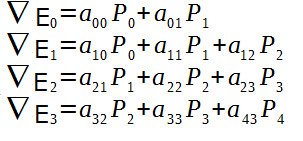
dynamics式を時間軸と3D空間で分離した結果、各頂点に対して一つの線形式で表すことができます。つまり、linear systemを取得できました。
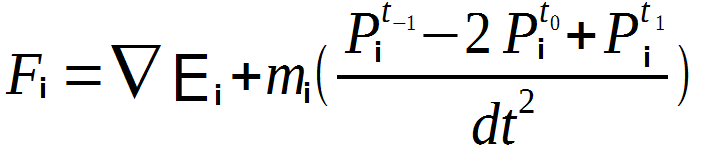
注目してほしい所が一つあります。エネルギーの勾配は3D空間(x,y,z)に対しての微分なので、時間の変数は自由です。線形システムを解決する時、【今のt】を使えばすぐにその頂点のエネルギーを計算することができます。そのapproachを持って求められた【次のt】の式はこの様になります:
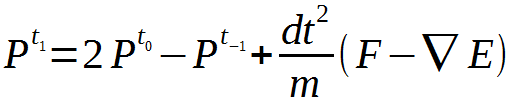
このapproachは陽解法(Explict Method)として知られています。実装はシンプルですが、精度は不十分です。非常に小さいtimestepを使わないと安定さを確保できません。さらに別のattribute値によって不安定になることもあります。
陰解法
精度が高くて安定している方法があります。それは陰解法(implicit method)です。陰解法ではエネルギーを求める時、【今のt】ではなく【次のt】の情報を使用します。【次のt】での頂点Pの位置は【次のt】での近傍にある頂点Pの位置に依存するようになります。線形システムを解決する難易度はあがりますが精度とtimestepの大きさのバランスを考慮すると陽解法よりメリットがあります。
陰解法にて得られた線形システムはこの形です:
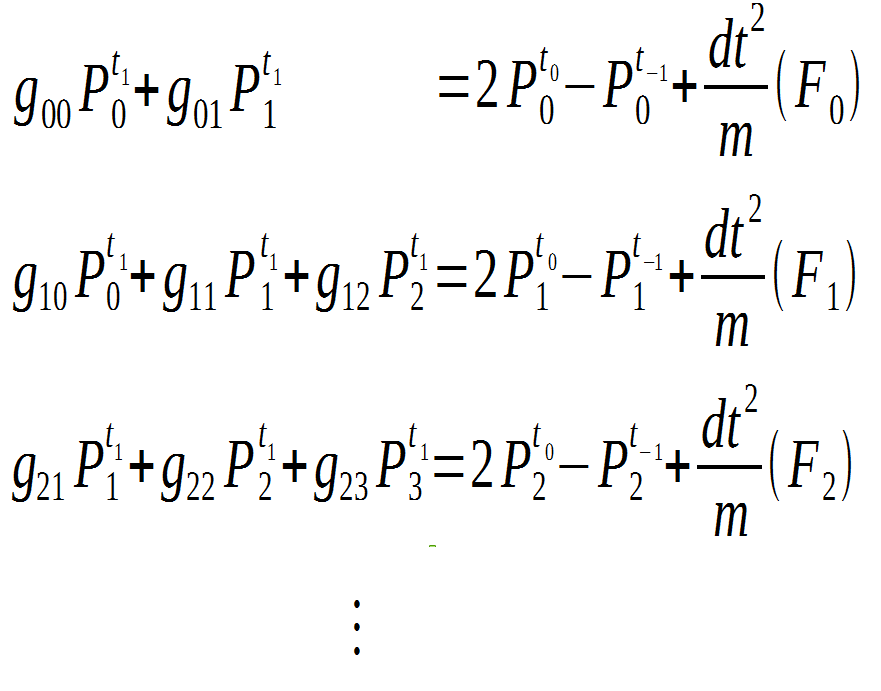
さらに、行列式として書き直せば、次になります:
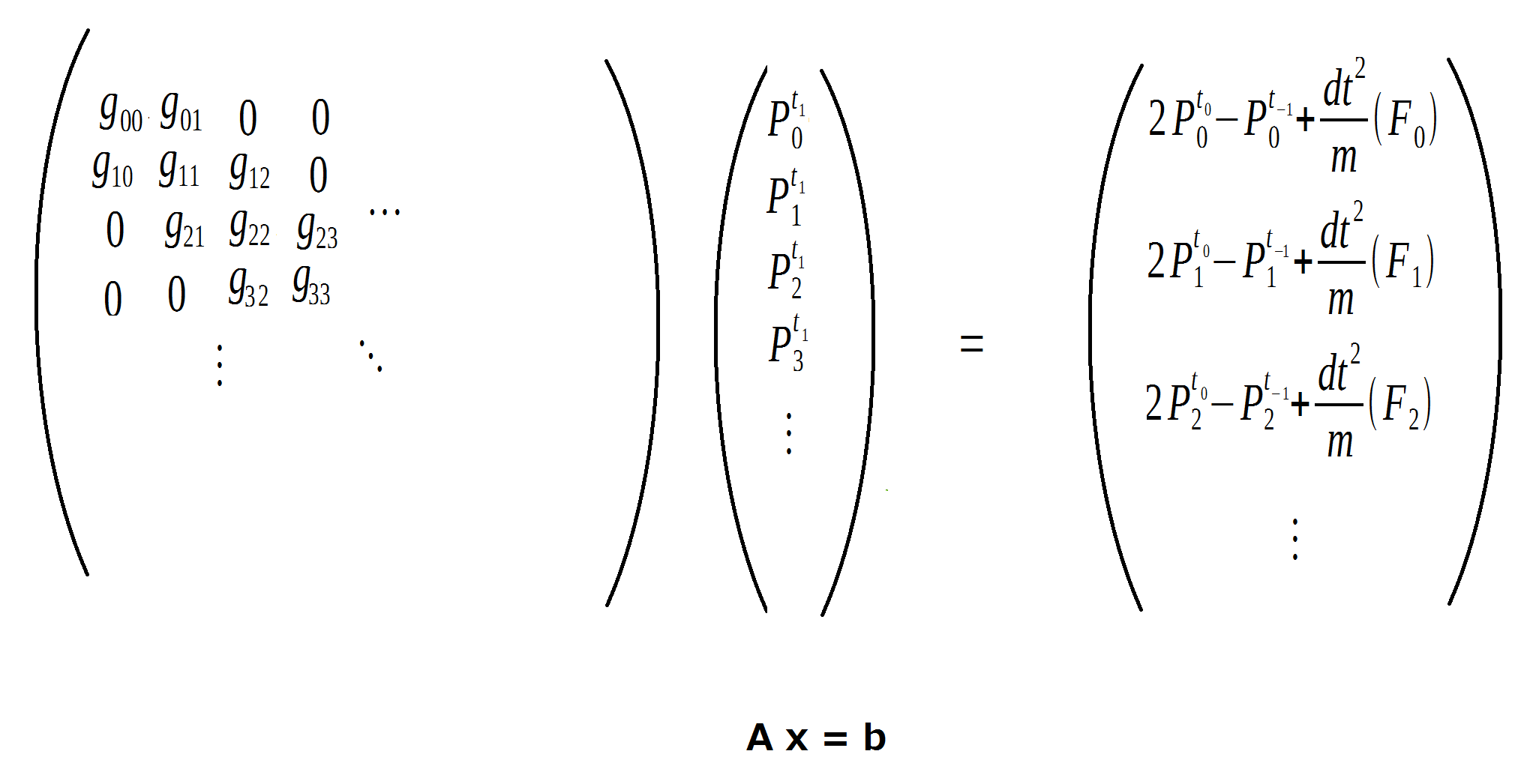
この様なシステムの解決について少し紹介させていただきたいとおもいます。
反復法
行列式で書き直すと解答は明らかになります。行列のAの逆行列を求めて両方を乗算すれば、【次のt】の形状が得られます。この様な方法は直接法(direct method)といいます。逆行列を求める為のコストは高く、この方法はあまり現実的ではありません。そのため直接法の代わりに、反復法(iterative method)がよく使われています。反復法は、初期に設定された解答を再計算しつつ、誤差を減少する方法です。計算の繰り返しで正しい解答を近似できます。反復法はあくまで近似を求めるので、スピードと精度のバランスを探すことが必要です。行列システムの反復はシミュレーションの反復の中で行われるので、行列の反復回数はperformanceに大きく影響します。
ヤコビ法
反復法はいくつかありますが、一つだけ紹介したいと思います。それはヤコビ法(Jacobi method)です。詳細はWikipediaを参照ください。
ヤコビの一つの利点としては並列化が容易なためGPU実装に向いているといえます。しかし他の方法と比べて精度の面ではあまり良くありません。その精度を高める為、conjugated gradientの様な別方法をappendできますが、内積の計算が多くて、GPU実装として不適切になります。そこで、この記事のメインとなる手法です!
Chebyshev法
Chebyshev法はヤコビ法の精度を高くした上で、必要な反復回数をかなり低下させられる手法です。さらに内積が不要なのでGPU実装にも最適です。Chebyshev法は数学界において昔から存在していましたが、CG業界においては比較的最近登場しました。2015年のSIGRAPPH ASIAで発表された論文は細かく説明されていますので、詳細を知りたい方は参考にしてみてください。ではなぜ今までCG業界であまり登場する場がなかったのかを説明させていただきたいと思います。 前述の通りChebyshev法の利点は大きいのですが、逆に大きな短所もあります。解決されている行列の max eigen value が必要です。 Eigen valuesを求めるのは、逆行列を求めるのと同様にコストが高いです。clothやsoft bodyをシミュレーションする場合、行列は大きくなりがちなためリアルタイムにmax eigen valueを求めるのは難しくなります。またHairをシミュレーションする場合、行列は小さいですがその数が多くなります。これらの理由からChebyshev法は今までCG業界であまり採用されてこなかったとのことです。
そんな中、2014年のSIGGRAPHで新たな論文が発表されました。Projective Dynamics (PD)という手法です。PDはこの記事で説明しているシミュレーションの方法に基づいています。一般のmass spring systemsやFEMなどはシミュレーションの反復毎に行列の更新が必要になりますが、PDではシミュレーションしている物体のtopologyが変わらない場合、行列は固定となります。つまり行列のeigen valuesを一回だけ求めればよいのでchebyshev法の短所を補うことができるようになりました。
以下のChebyshev法:有り・無しの結果をご覧ください。
| 本数 | 24570 |
| 総合頂点数 | 995032 |
| min 長さ | 7.28cm |
| min 頂点数 | 4 |
| max 長さ | 112.34 cm |
| max 頂点数 | 74 |
| timestep | 1 ms |
髪の毛のgeometry dataはコチラに提供されています。Long Straight hairというデータから24570本数のシミュレーション結果です。
ここまで紹介させていただいた物理シミュレーションのボトルネックは行列演算(Ax=b)です。 この結果からもヤコビ法のみを利用すれば反復回数が多くないと安定にならないので、シミュレーションは全体的に重くなります。Chebyshev法はこのボトルネックを直接高速化できる有効な方法です。
求める精度に寄りますが大きなperformance upが期待できる良い方法のひとつだと思います。
Code
Chebyshev法の実装は特に難しくはないです。GPU実装にする場合、細かい調整は必要ですが最終的に頂点毎に並列化できます。
Spectral Radiusというparameterはmax eigen valueです。それを求める為に、Eigenを使っています。
但し、Chebyshev法を使うには幾つか条件がありますので、導入する前に一度論文を参考にしてください。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | //solve the system Ax = b using chebyshev acceleration and pre-computed spectralRadiusVector solve(Matrix A, Vector b, float spectralRadius, int numIterations){Vector currentResult = b;Vector previousResult = b;Vector newResult;float omega = 2.0f;for (int i = 0; i < numIterations; i++){omega = 4.0f/(4.0f - spectralRadius*spectralRadius*omega);newResult = doJacobi(); //or could be any other methodnewResult = (newResult - previousResult) * omega + previousResult;previousResult = currentResult;currentResult = newResult;}return newResult;} |
皆さん、Chebyshev法いかがだったでしょうか?
もし固定した行列を扱っているのなら、この手法はとても有効だと思います。ぜひ利用してみてください。
今回は以上となります。次回はProjective Dynamicsの紹介をしたいと思います。楽しみにしていてください。
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください。


コメント
コメントフォーム