流体シミュレーションを使った自然現象の表現
2014/3/31
Tag: fluid,simulation
皆さん、はじめまして、開発室の川田です。
今回が始めての投稿と言う事で、自分が入社前から多少なりとも携わっている
CGにおける流体シミュレーションについて、表現が足りないところがあるかも
しれませんが、また、自分なりの言葉ですが紹介してみたいと思います。
流体シミュレーションを使えば、水、煙、火炎、雲や爆発などの
流体を表現することができ、最終的に映像化できます。

この画像は本文の直接的な例ではないですが、CGの流体シミュレーションで表現できる流体の
イメージとしての実写素材です。
CGにおける流体シミュレーション手法は、元々は数値流体力学、CFD(Computatinal Fluid Dynamics)
で使われていた流体計算の方法を、CG用に特化することで応用され、発展してきました。
ここでいう特化とは、試行錯誤のために流体シミュレーションをアニメータが何度も
実行できるように計算コストを抑えながら、かつ、映像表現において必要な確からしさ(リアルさ
とでも言うべきでしょうか)をもった流体挙動を、十分に得られるようにすることを指します。
また、近年は確からしい流体挙動の実現に加えてさらに、流体をアニメータが意図するよ
うに流体をより制御しやすくなるようにする技術も盛んに追求されており、この点もCG用の
流体シミュレーション手法の特徴と考えられます。
それに比べて、数値流体力学は例えば、数値計算の結果の厳密さに重きが置かれているよう
に思われます。
CG用の流体シミュレーションを使って得られた流体を、フォトリアルに可視化するための
レンダリング手法についても、非常に盛んな技術研究がなされています。
今回は流体の動き(アニメーション)を生成するために使用される、流体シミュレーション
の方法についてのみ述べます。流体シミュレーションを使うことでどのように
水や煙のアニメーションが作られるかを説明したいと思います。
流体シミュレーションで用いる方程式
CG用の流体シミュレーションで用いられる、流体現象を表現するための(支配)方程式
について、説明していきます。
この説明で、流体らしい動きをCGでどのように作り出しているかのイメージが、ある
程度分かっていただければ幸いです。
CG用の流体シミュレーションで用いられる手法には、流体を粒子表現する方法(パーティクルを
使った表現である粒子法)と、流体をボリューム表現する方法(格子法)の2つが主に存在します。
ここで、格子法とは流体を扱う空間全体を、ボクセルである格子で分割表現して、各格子の内部に
格納した速度、密度といった物理的な情報の変化を計算することで、流体のシミュレーション
を行う方法です。
一方、粒子法では、粒子一個一個自体が同様の物理的な情報を持っています。
どちらの手法にも利点がありますが、前者の格子法は例えば、渦巻くような動きの表現を比較的得意
とするため、煙といった表現でよく用いられます。
ただし、流体の存在しない領域も、基本的に格子ですでに表現されているため、メモリや計算コスト
を流体が存在しない部分でも必要となってしまうという状態が生じてしまいます。
また、格子以下のサイズの流れの情報は扱えないことになります。
一方、粒子法は例えば、流体の表面を様々な方法で比較的良く表現できるため、水といったものに
おいてよく用いられます。しかしながら、例えば、離れ離れになっている粒子をスムーズにつなげる
必要がある場合などは、工夫が必要となります。
いづれの方法でも、流体計算のために次のような数式が用いられています。
この式は流体の挙動を記述する方程式で、ナビエ・ストークス方程式と呼ばれ、数値流体力学
でもともとは用いられてきたものです。
この方程式を、以下で説明していくような形でCG用に用いることで、流体のアニメーションを作
り出します。
また、今回は格子法において特に、どのようにこの方程式が使われているかを説明してみます。
格子法
格子法で流体のアニメーションを作り出す際には、扱う領域内の各格子が、上の方程式中の記号
で表されるような物理量を持つことになります。
これらの方程式を何度も繰り返し解いて、各格子の値を何度も更新することで、空間全体の値が
徐々に変化していきます。
方程式を解く回数(ステップ数)としては、基本的には少なくとも、作りたい流体のアニメーションの
フレーム数が必要になります。
方程式を解くことで特に、各格子の速度の値が変化していくことになります。
その結果として、空間全体の速度場が変化していきます。
そして、この速度場の変化に伴い、空間に存在する(流体を表現する)密度(水、煙など)が運ばれて
流動して行き、これにより、最終的に流体アニメーションを作り出すことができるようになります。
便宜上、2つ目の式から説明していきます。また、説明の内容は Stable Fluid と呼ばれる
代表的な流体シミュレーションを参考にしながら、書かせていただきました。
非圧縮条件の式
まず、2つ目の式は質量保存を表現する式で、この式によって非圧縮性の流体を表現します。
ここで、非圧縮性の流体とは、密度が基本的には変化しない流体のことで、水や空気などがその代表例です。
ですので、この2つ目の式が表現しているのは、密度の流出入の合計が0(右辺の通り)になるということで、
結果として、流体の密度を一定にします。
この式では変数として、密度ではなく速度が書かれてありますが、速度の流出入量が同じということは、
(速度によって運ばれる)密度の流出入量が同じということになるので、このような式となっていると
考えられます。
運動量保存の式
次に、1つ目の式は、左辺については速度の時間ごとの変化を表し、また、右辺については左から順に、
移流項、圧力項、拡散項、外力項という要素で構成されます。
格子法におけるCG用の流体シミュレーションでは、これらの項を順に解いて、2つ目の式を解いていきます。
順に解く理由は、式を一度に解こうとすると計算が複雑で、計算コストが非常に高くなってしまうからです。
一方、順に解いてもCGの用途における計算精度を得るには十分で、確からしい流体挙動が得られると考えられます。
また、一度に解かない方が、計算は一般的には安定することになります。
さらに、特に外力項など(例えば風の効果を表現する)のようにアニメータが直接、特定の項を調整したいときなど
にも便利で、自由な調整や制御もとても重要なCG用の流体シミュレーションでは、このことも式の項を順に解くと
いう考え方の利点と思われます。
また、2つ目の式は、1つ目の式において圧力項を解くときに用いられます。
以上のように、2つの式を計算することで、各格子の速度を求めて、領域全体の速度場を更新していくこと
になります。
1つ目の式を構成する各項について、数式の細かい説明よりもむしろ、各項がどのようなことをしているかのイメージ
が少しでも分かるように、以下で順に書いていってみることにします。
移流項
(上の赤枠でハイライトした)1つ目の式の右辺における最初の部分である移流項は、流体が速度に沿って移動していく
という現象を表現しています。
川で渦が流れに沿って移動していくのに気がつかれたことがあるかもしれませんが、渦のような速度のかたまり
自体も実は移動しており、速度が周囲の影響を受けながら刻一刻と変化してく様子を、この項によって表現するこ
とが可能になります。このような現象による速度の変化を領域全体について計算し、移流によって起こる
領域全体の速度場の変化を求めているのがこの移流項です。
また、格子法での流体シミュレーションでは、セミ・ラグランジュ法という方法を用いており、現在のステップの
各格子へと流体が移動してきていると考え、各格子へと移動してくる元の格子の速度の値が何であるかを、
たどって計算します。
このようにして、前のステップの状態を考えながら逆算的な操作を行うことになるので、移流項の計算が安定します。
計算が安定するというのは利点ですが、セミ・ラグランジュ法の計算にはその性質上、従来は数値の誤差が発生して
しまっていました。
そして、その誤差により計算精度が落ちるため、流体が動いていくときに本来は生じるはずの細かい挙動の情報が失われ
てしまっていました。そのような情報の代表的なものに、細かい渦の挙動があります。
これに対して、そのような数値誤差を補うために、様々な手法が現在までに提案されています。
例えば、Vorticity Cofinement と呼ばれる方法は、速度場において渦を検出して、その渦情報を強めて
(情報が失われている)速度場に追加するという処理を行います。これによって、数値誤差が軽減されることになります。
Vorticity Cofinement のような方法を使うと渦の強めかたを設定したりすることが出来て、ユーザがどのような
渦の度合いを持つ流体を生成したいかを調整するという制御の意味でも、重要な手法だと思われます。
また、セミ・ラグランジュ法の詳細については、余力がありましたら調べてみて頂ければと思います。
圧力項
(上の赤枠でハイライトした)2つ目の圧力項は、流体はその圧力が高いほうから低いほうへと、圧力を均一化す
るように移動していくという現象を表現しています。
また、流体が移動するということは、そこに速度が生じることになります。
ですので、圧力項では、このような圧力の変化によって生じる速度の変化を領域全体について計算し、領域全体
の速度場の変化を求めます。
2つの異なる温度を持つ2種類の流体が、時間の経過とともに、2つの温度の間の温度へと遷移していくのも、
均一化の一例です。
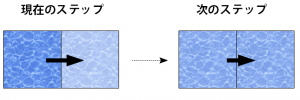
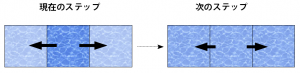
圧力の高い左側の格子から、圧力の低い右側の格子へと流れが移動するような速度が生じて、その状態でステップ
が進むことで圧力が均一化していく様子を、色の濃さで表現したものが以下の模式図(圧力項)です。
この圧力項を解く際に、2つ目の非圧縮条件の式を利用します。
その理由は、密度が一定であるという1つ目の式の条件を、圧力項の部分に適用しながら、圧力の変化が均一化
するようにすることで、式が解けるからです。
すなわち、圧力が一定になるような速度を求めてあげれば、そのような流体は密度が一定であり、非圧縮性が
満たされることになります。
よって、圧力項で、そのような非圧縮性が満たされる流体になるように式を解くことで、非圧縮性の流体が持
つ特徴である、渦巻くような挙動を表現することが可能となります。
ここで、圧力を一定にするような速度場を領域の全格子について求めるとき、ポアソン方程式と呼ばれる
巨大な行列式で記述される式を解くことになります。この行列式を解くには高い計算コストがかかるため、
この式を効率的に解くといった技術研究も盛んに行われています。
ポアソン方程式についての詳細は、また余力がありましたら調べてみて頂ければと思います。
また、格子法の圧力項の計算は非圧縮条件を考えているため、渦巻くような挙動を生成するのに適しているという
利点がある反面、流体の動きや方向の制御を行うことは簡単ではありません。
なぜなら、圧力項では、圧力の変化が均一化するように各格子の周辺情報を常に考慮しながら、計算を行なわなけ
ればならないため、速度場の小さな変化が結果的に全体の挙動に影響を及ぼすことになるからです。
ですので、アニメータが流体の動きや方向を、部分的に調整するだけでも全体への影響が大きくなるため、
制御が簡単ではなくなることになります。
また、同じような理由で、空間全体を表現している格子の分割数を変えてしまうと、流体の動きが大きく変わってしまいます。
したがって、分割数を細かくして、最終的な結果としてより詳細な流体を得ようとしても、細かくする前の動きとは大きく
異なるという状態が生じてしまうことが少なくありません。
このような格子法の制御や格子の分割に関する難しさに取り組んだ技術についても、多くの研究が行われていますので、
機会があれば説明できればと思います。また、余力がありましたら調べてみて頂ければと思います。
逆に、この項の圧力に関係する物理量を操作することで、部分的に大きな圧力を意図的に作り出して、その部分を起爆源として
爆発のような劇的な、高速で流体が伝播するといった効果を得ることも可能です。
拡散項
(上の赤枠でハイライトした)3つ目の拡散項は、流体が周囲に広がる形で、なじんでいく様に移動していく現象を
表現しています。
タバコなどの煙が時間が経つと薄くなりながら、周囲に溶け込んでいく現象を想像すると分かりやすいのではと
思います。
真ん中の格子から、左右の格子へと(速度を含めた)流れが移動して、次のステップでは流れが周囲になじんでいるという様子を、
色の濃さで表現したものが以下の模式図(拡散項)です。
この拡散項では、各格子における周辺の格子の方向へ、1ステップあたりどのぐらいの流体が移動していくかを計算
します。そのようにして、流体の移動量を領域全体について計算し、拡散によって起こる領域全体の速度場の変化
を求めます。
この項についても、圧力項で説明したポアソン方程式を解く必要があるので、煙などで周囲への溶け込みの度合いが
強いもの以外は、省略されることもあります。
また、液体の場合には、この項目の動粘性係数を大きくすることで、流体が移動していくときの抵抗力を表現できます。
したがって、例えば溶岩のようなネバネバした流体を表現することも可能になります。
外力項
(上の赤丸でハイライトした)最後の外力項は、流体に外部から色々な力が加わることで、流体が様々な影響を受ける
という現象を表現しています。
その代表的なものに重力があり、(すでに説明した)外力項以外の項で計算した流体の動きに加えてさらに、流体が
自身の重さで落下するという挙動を表現できます。
このように流体に加わる力を(外力が全体に適用されている場合は)領域全体について計算し、外力によって引き起こ
される、領域全体の速度場の変化を求めます。
また、外力(ベクトル)には大きさと方向の情報があり、各格子がこれらの情報を保持することになります。
さらに、重力とは逆の、鉛直上方向に働く力として浮力があります。
浮力は一般的には、流体が持つ温度を基に計算し、周囲よりも温度が高ければ高いほど流体は上昇していきます。
爆発によって生じた火炎がその非常に高い温度により、きのこ状になりながら上昇していく現象を想像すれば、
分かりやすいかもしれません。
また、最初に説明したように、風の効果などをアニメータが表現したい場合は、直接この項のみを調整することで
その効果を適用すれば良いことになります。
流体の動きの条件の設定と流体の制御
外力によって、流体がどのように動き始めるかといった条件を設定することもできます。
逆に言うと、外力によって計算領域がどのような条件下にあるかが設定されれば、この設定を基にして、外力項以外の項が
流体の挙動を基本的には自動的に決めることができるようになります。
さらに言えば、流体の発生源であるソースとして、すなわち、物が燃えている熱源から煙が昇ってくるとか、水が流れ出して
くる滝の元などをアニメータが外力項によって設定して表現します。
そして、その設定を基に流体が動き始めるきっかけが与えられれば、外力項以外の項目が、火炎や煙、あるいは水といった
各流体の流れるような、あるいは、渦巻くような挙動を生成してくれることになります。
もちろん、外力項以外の項の物理量を設定して、流体の挙動を決めることは可能ですが(例えば、粘性の強さや非圧縮
の度合い等)、外力項によって流体を動き始めさせることが基本的には必要となります。
さらに、制御という観点についても考えると、このような外力を用いて、流体を特定の形状に維持したりといったこと
が可能となります。映画等で、人間のような形状をした水が川から現れてくる、といった場面を見たことがあるかもしれません。
例えば具体的には、目標とする特定の形状における表面の情報、例えば表面の法線を外力の方向として用いて、形状の中心へと
向かうような力を加える形で、制御を行います。
流体の周囲に広がっていくという基本的な性質上、何も外力を加えないと徐々に通常大きくなって形状からはみ出していく
のですが、このように外力を利用することで、形状の内部にある程度流体が収まるようにすることも可能となります。
このような外力による流体の形状の制御と、流体の自然な動きにはトレードオフの関係がありますが、リアルであり、かつ
印象的な映像の演出のために、この2つをできるだけ両立させるようにする技術研究も長年に渡って盛んです。
密度の移動の計算
以上のように2つの式を組み合わせながら、しかも、移流項、圧力項、拡散項および外力項を順に毎回、各ステップにおいて
計算します。
これにより、移流項、圧力項、拡散項および外力項によって表現される、流体に関する物理現象を考慮した速度場が各ステッ
プで求まるので、時間の経過と共に動いていくときの、流体挙動を表現することができることになります。
また、これまでに説明した式で、流体を移動させるための速度場をステップごとに計算することは可能になりましたが、移動する
流体自体を表現するような流体の密度も、設定する必要があります。
密度の設定は例えば、計算領域において密度を配置したい場所を、アニメータが指定することで可能になります。
外力項での流体のソースについての例で、熱源と同じ場所に、密度を配置するというような場合を考えると、分かりやいのではと
思います。このような指定をすると、熱源の外力によって移動が開始し、ステップごとにその後更新されていく速度場に
沿って、熱源の密度が移動していくというような流体のアニメーションが出来ることになります。
このようにして配置した密度を、速度場によって移動させるとき、その移動の計算には上で説明した移流項を用います。
上の移流項においては移動させる物理量が速度であったのに対して、こちらの移流項の計算では、移動させるものが密度という
違いはありますが、それ以外は基本的に同じです。
火炎などを扱う場合には温度も必要となりますが、その場合も同様に、上の移動させる密度を温度に変えることで表現可能と
なります。
長くなりましたが、以上のように、流体シミュレーションの方程式を解くことで、空間全体の速度場の変化を求めて、
そして、配置した密度(あるいは、温度など)が速度場によって運ばれて流動していきます。
さらに、密度を表現する流体の性質(煙であるか火炎であるかなど)に応じて、ボリュームレンダリング等を行います。
これにより、最終的に流体のアニメーションが得られることになります。
最後に
終わりに近づきましたが、説明したような流体シミュレーションを用いて、多種多様な自然現象を表現することが
可能となります。
上で挙げたもの以外にも燃料等といった物理量を追加することで、火炎といった表現も可能になりますし、
気化や熱といった物理モデルを追加することで雲のような現象も実現されています。
また、物体との干渉についても考慮することで、物に影響を受けて生じる渦などの挙動も表現可能になります。
さらに、乱流といった流体の動きに関するより複雑なモデルを導入することで、実際の物理現象により近い
挙動を持つ流体のアニメーションを作り出すことが可能になります。
これらについては今回は説明できませんでしたが、流体シミュレーションを実装したコードが、いろいろと
ネット上で公開されていますので、それらに触れてみることでCGにおける流体シミュレーションの中身や
応用例がさらに理解しやすくなるのではと思います。
※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください。

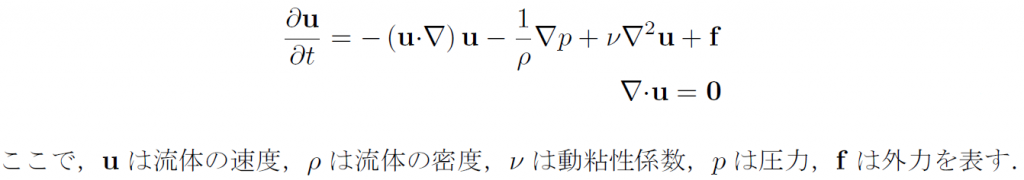
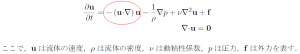
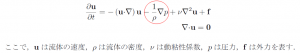

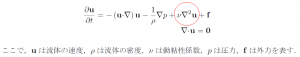
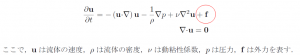

[…] ある程度説明しているので、 [DF_talk] 流体シミュレーションを使った自然現象の表現 […]
Posted at 2014.09.3 12:02 by デジタル・フロンティア-Digital Frontier | DF TALK | 流体シミュレーションのアップレゾ(高解像度化)について