株式会社デジタル・フロンティア-Digital Frontier

Header

Main

DF TALK

  • TOP
  • DF TALK
  • IFSフラクタルで自然現象を表現しよう

IFSフラクタルで自然現象を表現しよう

2014/1/6

Tag: ,,

あけましておめでとうございます。開発室の高山です。
前回は数式が並んで絵的に地味だったので、今回は絵で見て楽しめるものとしてIFSフラクタルの話でも。

今回も出てくるコードは全てVisual Studio C++で書かれたものです。

IFSフラクタルとは

IFSフラクタルは反復関数系(Iterated Function System)によって描かれたフラクタルの事です。
ここで言ってるフラクタルとは自己相似性を持つ図形のことで、部分と全体で同じ構造をしているものです。
文章で説明しても分かりにくいと思うので、まずは一例を。

シェルビンスキーのギャスケット
この図形は見た事がある方も多いのではないでしょうか。
このように部分と全体で同じ構造をしているものをフラクタル図形といいます。
ちなみにこの図形にはシェルピンスキーのギャスケットという名前がついています。かっこいい。

フラクタル図形には様々な種類がありますが、
実世界でも植物や氷の結晶、海岸線などフラクタル図形として近似的に表現できるものは様々あります。
そこで今回はそれらをIFSフラクタルを用いて簡単に実装してみよう！というお話です。

IFSフラクタルの考え方

IFSフラクタルを端的に説明すると、
１．画像全体をコピーして、
２．適当なサイズで適当な位置に適当な向きで貼り付ける
３．１→２を繰り返す
こんな感じです。

ただ、２．の貼り付け方が１パターンだとあまり複雑な図形はできないので、複数パターン用意するのが一般的です。
では図を入れた説明を。

まずこれが元画像。左下に１点だけあります。

これをコピーして３パターンの方法で貼り付けたのが下の画像です。

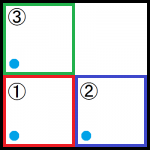
①の赤い枠が１つめのパターンで、移動はせずに縮小だけした場合です。
②の青い枠が２つめのパターンで、右に移動して縮小したものです。
③の緑の枠が３つめのパターンで、上に移動して縮小したものです。

この処理により、黒枠の中には３点ある事になります。これをまたコピーして同じように３パターンで貼り付けます。

さらに繰り返します。

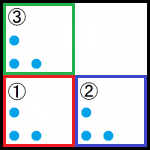
最終的にはこのような形になります。さきほどのシェルピンスキーのギャスケットを横によせた感じになりました。

IFSフラクタルの実装

では実装してみましょう。
上では画像全体をコピー→貼り付けと書きましたが、実装する場合には画像上に大量の点を配置し、
それをそれぞれ動かして描画していくことが多いです。

コードは以下のようになります。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <math.h>
#include <stdlib.h>
using namespace System::Drawing;
using namespace System::Drawing::Imaging;
#define M_PI 3.14159265358979323846
 
int MAXP = 100000; // 頂点数
int MAXR = 30; // 繰り返し回数
int WIDTH = 400; // 横幅
int HEIGHT = 400; // 縦幅
int POW = 400; // 倍率
 
int setX, setY; // 描画時のX, Y座標
double x, y, new_x, new_y, sx, sy, th, tx, ty, rnd;
 
Bitmap ^bmap = gcnew Bitmap(WIDTH, HEIGHT);
 
// IFSフラクタル(シェルピンスキーのギャスケット)
for(int n=0;n<MAXP;n++){
    x = 0.0; // 最初のX座標
    y = 0.0; // 最初のY座標
     
    for(int t=1;t<MAXR;t++){
        // 0～30までの乱数
        rnd = (double)rand() / RAND_MAX * 30.0;
 
        if(rnd < 10.0){ // 上の部分
            sx = 0.5; // 拡大率(X方向)
            sy = 0.5; // 拡大率(Y方向)
            th = 0.0; // 回転角度
            tx = 0.0; // 移動距離(X方向)
            ty = 0.0; // 移動距離(Y方向)
        } else if(rnd < 20.0){ // 左下の部分
            sx = 0.5;
            sy = 0.5;
            th = 0.0;
            tx = -0.25;
            ty = 0.5;
        } else { // 右下の部分
            sx = 0.5;
            sy = 0.5;
            th = 0.0;
            tx = 0.25;
            ty = 0.5;
        }
         
        // 点の移動（アフィン変換）
        new_x = sx * cos(th) * x - sx * sin(th) * y + tx;
        new_y = sy * sin(th) * x + sy * cos(th) * y + ty;
        x = new_x;
        y = new_y;
         
        // 画面のサイズに合わせる
        setX = (int)(x * POW + WIDTH / 2);
        setY = (int)(y * POW);
 
        // 画面内にいる場合、描画
        if(setX >= 0 && setX < WIDTH - 1 && setY >= 0 && setY < HEIGHT - 1){
            bmap->SetPixel(setX, setY, Color::FromArgb(255, 255, 255));
        }
    }
}
 
// 画像出力
bmap->Save("result.bmp", ImageFormat::Bmp);

これは最初にあげたシェルピンスキーのギャスケットを描画するものです。
乱数によってどのパターンの動きをするのか決定し、
sxとsyで拡大縮小、thで回転、txとtyで移動の値をそれぞれ決めて新しい座標を求め、
貼り付けて(描画して)います。

では自然物っぽい例も。下のコードは氷の結晶的なものを描画するコードです。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
MAXP = 100000; // 頂点数
MAXR = 6; // 繰り返し回数
POW = 300; // 倍率
 
// IFSフラクタル（氷の結晶）
for(int n=0;n<MAXP;n++){
    x = 0.0; // 最初のX座標
    y = 0.0; // 最初のY座標
     
    for(int t=1;t<MAXR;t++){
        rnd = (double)rand() / RAND_MAX * 100.0;
 
        if(rnd < 60.0){ // 10% * 6 周りの６点
            sx = 1.0 / 3.0;
            sy = 1.0 / 3.0;
            th = theta;
            tx = 1.0 / 3.0 * cos((int)(rnd / 10.0) * M_PI / 3.0);
            ty = 1.0 / 3.0 * sin((int)(rnd / 10.0) * M_PI / 3.0);
        } else { // 40% 全体の縮小図
            sx = 0.5;
            sy = 0.5;
            th = theta;
            tx = 0.0;
            ty = 0.0;
        }
 
        new_x = sx * cos(th) * x - sx * sin(th) * y + tx;
        new_y = sy * sin(th) * x + sy * cos(th) * y + ty;
        x = new_x;
        y = new_y;
 
        setX = (int)(x * POW + WIDTH / 2);
        setY = (int)(y * POW + HEIGHT / 2);
 
        if(setX >= 0 && setX < WIDTH - 1 && setY >= 0 && setY < HEIGHT - 1){
            bmap->SetPixel(setX, setY, Color::FromArgb(0, 128, 255));
        }
    }
}

氷の結晶は六角形のものが多いので、それを表現するために六角形の頂点に縮小コピーを貼り付けています。
これを実装した結果が以下の通り。

なんとなくそれっぽくなったのではないでしょうか。

動画への拡張

これをちょっと拡張すればなんと動画もできてしまいます。IFSフラクタルすごい。
やり方は単純で、フレームごとにパラメータを連続的に変えていけばそれっぽくなります。
例としてシダ植物を動かしてみた結果が下の動画（クリックで動作）です。風に揺られている感じが表現できていませんか？

コードは以下の通りです。
静止画から動画にする必要があるためfor文が一つ増えています。
一番大きいパターンの回転角度をフレームによって変えていく事で、ゆれを表現しています。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
MAXP = 100000; // 頂点数
MAXR = 30; // 繰り返し回数
POW = 40; // 倍率
 
for(int f=0;f<1000;f++){
    Bitmap ^bmap = gcnew Bitmap(WIDTH, HEIGHT);
 
    theta = 0.01f * sin((float)f * 3.0f * (float)M_PI / 180.0f) + 0.02f; // 角度
 
    // シダ植物
    for(int n=0;n<MAXP;n++){
        x = 0.0; // 最初のX座標
        y = 0.0; // 最初のY座標
     
        for(int t=1;t<MAXR;t++){
            rnd = (double)rand() / RAND_MAX * 100.0;
 
            if(rnd > 15.0){ // 85% メインの部分
                sx = 0.85;
                sy = 0.85;
                th= -theta;
                tx = 0.0;
                ty = 1.6;
            } else if(rnd > 8.0){ // 7% 左側
                sx = 0.3;
                sy = 0.3;
                th = -1.0;
                tx = 0.0;
                ty = 0.44;
            } else if(rnd > 1.0){ // 7% 右側
                sx = 0.3;
                sy = 0.3;
                th = 1.0;
                tx = 0.0;
                ty = 1.6;
            } else { // 1% 茎の部分
                sx = 0.0;
                sy = 0.16;
                th = 0.0;
                tx = 0.0;
                ty = 0.0;
            }
  
            new_x = sx * cos(th) * x - sx * sin(th) * y + tx;
            new_y = sy * sin(th) * x + sy * cos(th) * y + ty;
            x = new_x;
            y = new_y;
         
            // 画面のサイズに合わせる
            setX = (int)(x * POW + WIDTH / 2);
            setY = (int)(HEIGHT - y * POW);
 
            if(setX >= 0 && setX < WIDTH - 1 && setY >= 0 && setY < HEIGHT - 1){
                bmap->SetPixel(setX, setY, Color::FromArgb(0, 128, 0));
            }
        }
    }
     
    // 画像出力
    bmap->Save("result" + f.ToString("00000") + ".bmp", ImageFormat::Bmp);
    delete bmap;
}

他の例も。先ほどの氷の結晶を無理やり動かしてみたのがこちら。

なんか別物になりましたが、これはこれでありじゃないでしょうか。

時間や繰り返しごとに色を変えていくとこんな表現も出来ます。

IFSフラクタルは制御は難しいかもしれませんが、様々な表現が出来る可能性を秘めています。
パラメータを色々変えてみて、オリジナルの表現を見つけてみてはいかがでしょうか。


　※免責事項※
　本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
　これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
　自己責任でご使用ください

コメント

コメントはありません

コメントフォーム

CAPTCHA

*

コメントは承認制ですので、即時に反映されません。ご了承ください。

CAPTCHA


 

タグクラウド

月別アーカイブ

2025年

2018年

2017年

2016年

2015年

2014年

2013年

2012年

2011年

2010年

Footer