スプライン曲線の話
2013/12/10
どうもお久しぶりです。DF一(いち)のゆるふわ系こと松岡です。
今回はスプライン曲線の話をします。
スプライン曲線
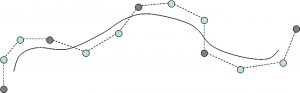
スプライン曲線とはコントロールポイント(以下CP)と呼ばれる点で定義されるカーブです。
CGやCADでは、たとえば、モデリングやパラメータの補間など、いろいろな用途に使われています。
スプライン曲線の種類
さてスプライン曲線というと、一般的に知られているのは、以下のようなものがあります。
- Bezier曲線
- B-Spline
- Nurbs
- Catmul-Rom曲線
これらはぞれぞれ異なる特徴を持っていて、使い分けられていますので、一通りの説明していきます。
Bezier曲線
おなじみBezier曲線ですね。
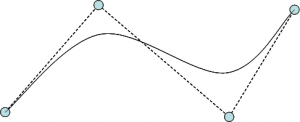
たとえば、3次のBezier曲線は4つのCPにより端と端をつないだ曲線になっています。
Bezier曲線は一般には以下のように定義されます。
ここで、
P(t):曲線
Pi:i番目CP
B(t):バーンスタイン関数
N:CPの数
です。
バーンスタイン関数は以下のように定義されます。
Bezier曲線にかぎらず、スプライン曲線は、次数というのが大きな要素です。
同じ種類のスプライン曲線でも次数が異なれば正確に変換することは不可能ですが、次数が一致していれば異なる種類のスプライン曲線でもある程度変換可能だからです。
次数とは0から1まで可変する自由変数(上記の定義ではt)での最大の乗数を指します。
たとえば上式で3次のBezier曲線は以下のような式で表せます。
ここでtについてる最大の乗数が3ですので、次数も3となります。
Bezier曲線では、この次数はCPの数とも関係します。
3次のBezier曲線では、CPの数は4つです。
次数+1=CPの数の関係が成り立ちます。また次数+1を階数と呼ぶこともあります。
つまり3次のBezier曲線は4階のBezier曲線ということができます。
Bezier曲線の特徴は
- 最初の点と最後の点に曲線が通る
- 凸閉包性がある
- その曲線は必ずCPで囲んだ凸包図形の内側に生じる
- アフィン不変性がある
- マトリクスで変形(アフィン変換)したCPから求めた曲線と曲線の軌跡をマトリクスで変形したものとが一致する
などがあります。
以上の特徴のから、Bezier曲線はCPから曲線の軌跡が想像しやすいため、人間・アプリケーション双方から扱いやすく、曲線を表現する手法として一般的なものとなっています。
ちなみに次数に関して多くのアプリケーションでは3次のものが使われます。(例外的にAdobeのFlashは2次のBezier曲線が使われているようです)
B-Spline曲線
Bezier曲線の問題点はCPを増やすと、コントロールしにくくなり、計算量も増えてしまうことです。
たとえば、Bezier曲線では、以下のように最初のCPを動かすと、最後のCP付近の曲線も動いてしまいます。
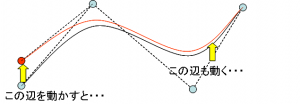
また、CPを増やすとその分曲線の次数も上がり、計算量が増えてしまいます。
このため、Bezier曲線は、CPを多くしたい場合・長い曲線を表現したい場合に不適となります。
B-Spline曲線では上記の不具合をノット列というものを導入することによって解消したものです。
B-Spline曲線の定義は以下のような形になります。
B-spline基底関数を以下のように定義します。
ここで、
P(t):曲線
Pi:i番目CP
bj:B-spline基底関数
n:次数
m:knotの数
です。
ちなみにknotの数、次数、CPの数は以下の関係にあります。
knotの数 = 次数+1 + CPの数
B-Spline曲線はノット列によって形状を変えることができます。
例えばノット列を以下のように定義したとき、
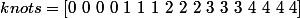
その曲線はBezier曲線をそのまま並べたようなものにすることができます。
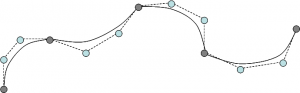
以上では、並べたBezier曲線の間が折れてしまって連続性がありません。これはCPの位置はそのままでノット列を変えてあげることで滑らかな曲線に変えることができます。
以上のようにB-Spline曲線は、ノット列によってBezier曲線を並べた以外の曲線を表現することが可能です。
B-Splineの特徴は
- 次数をそのままでCPの数を増やすことが可能
- ノット列を調整することで曲線の形を変えることが可能
となります。
Nurbs
NurbsはNon Uniform Rational B-Splineの頭文字をとったものになります。
日本語に訳すと、非均一有理Bスプラインといったところでしょうか。
B-Spline曲線をさらに拡張したものです。
Nurbsの関数は以下のように定義されます。
ほとんど、B-Spline曲線と同じですが、ここで注目することは重みwiをもつことです。
以上のように重みwiを持つものを有理関数といいますが、これによって非有理のBスプラインでは正確に表現できない曲線が表現できるようになります。
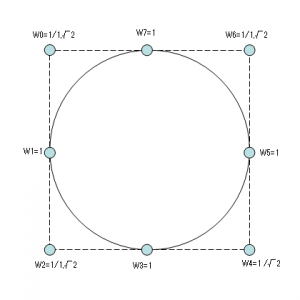
例えば円は非有理のB-Spline曲線では表現できませんが、NURBSでは表現できます。
Nurbsの特徴は以下のようになります。
- B-Spline曲線のコントロールポイントに重みWiを持たせたものになります。
- 円なども表現できる。
catmull-romスプライン曲線
上記までの曲線は必ずしもコントロールポイントを通りません。
一方でコントロールポイントを必ず通るような曲線をカーディナルスプラインと呼びます。MS-Officeなどの作図ツールではこのカーディナルスプラインが使われています。
カーディナルスプラインは一種類ではありませんが、代表的なものにcatmull-romスプライン曲線があります。このスプラインは3次(4階)です。
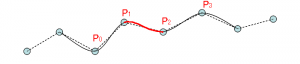
4つの点P0,P1,P2,P3を通るcatmull-romスプライン曲線は以下の式の通りとなります。
これでP1からP2にかけてカーブが定義されます。
複数のCPから曲線を定義したい場合は、CPの番号をひとつずつずらしたものを用います。
Catmull-Romスプライン曲線の特徴は
- CPを曲線が通る
- 常に滑らかな曲線となる
などです。
スプライン曲線の使い分け
ここまで、いろいろなスプライン曲線を見てきましたが、
結局どのスプラインを使ったらよいのかという疑問を抱くかもしれません。
それぞれのスプライン曲線は得意不得意があります。
このため、用途によって別の種類が使われます。
といっても、各スプライン曲線をコンバートできれば便利です。
実は各スプライン曲線は次数さえ同じであれば基本的に変換可能です。(ただし、有理曲線から非有理の曲線への変換は不可能)
変換できる関係を表すと以下のようになります。
NURBS<-B-Spline<-Bezier<->Catmull-Rom
これを利用すれば、任意の点を通るNURBSの作成が可能になります。
つまり、任意の点を通るようCatmull-Romスプラインで曲線を定義します。これを
Catmull-Rom曲線→Bezier曲線→B-Spline曲線→NURBS
の順番で変換可能していけばよいわけです。
終わりに
各種スプライン曲線を説明しました。
各種スプライン曲線の特徴を捉えれば、開発者はアプリケーションにカーブの組み込みが必要となった際、適切なものを選択できるかと思います。
また、ユーザーは既存アプリケーションでのカーブのコントロールもしやすくなるかもしれません。

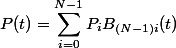
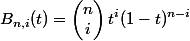
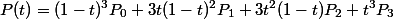
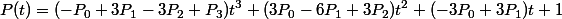
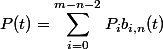
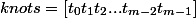
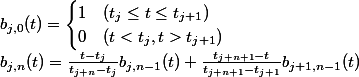
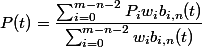
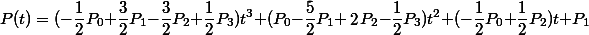
コメント
コメントフォーム