ポリゴンの体積を求める（Python Tipsおまけ付き）

2013/9/2

Tag: maya,python,tips

開発室の田村です。今回はポリゴンの体積を求める方法を紹介したいと思います。

ポリゴンの体積計算は空気の詰まった風船のようなオブジェクトで体積を一定にさせる時に用いられます。もしかすると筋肉等の表現に応用できるかもしれません。またある範囲の空間をオブジェクトが満たしているか、簡単に調べて高速化する手法を見たことがあります。

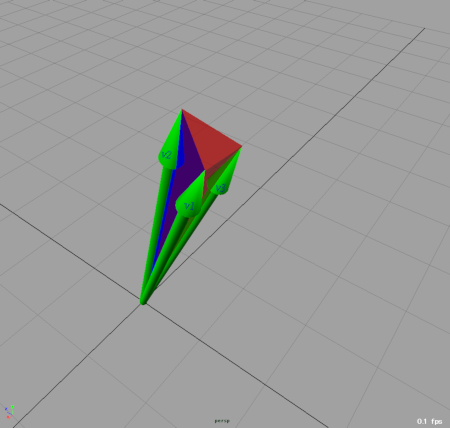
右のようなポリゴンオブジェクト（A）があったとします。このポリゴンオブジェクトは閉じてさえいればドーナツのように穴が開いていても構いません。法線は全て外側を向いていなければなりません。

体積を求めたいポリゴンオブジェクト

このようなポリゴンオブジェクト（A）の体積を求めるには、原点に頂点を一つ追加して、次のようにアイスクリームの乗ったコーンカップのようなポリゴン形状(B)を考えます。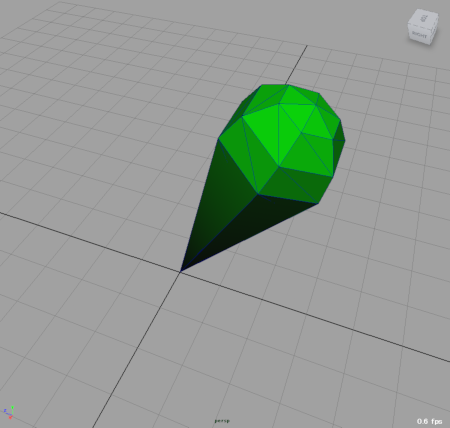

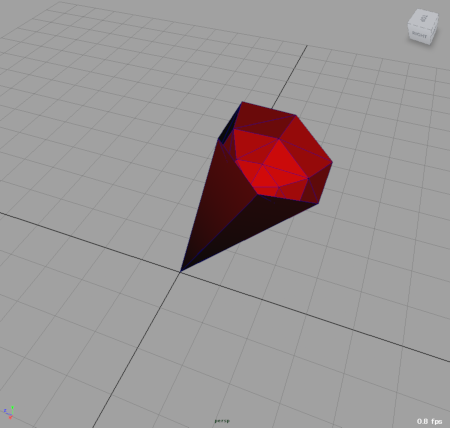
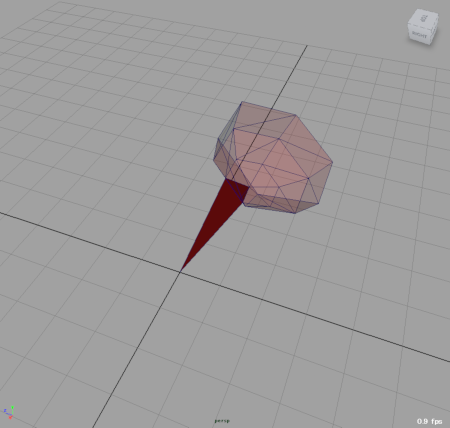
この形状の体積からコーンカップだけの形状(C)の体積

を引くと、（A）の体積=（B）の体積-（C）の体積となって元のポリゴンオブジェクトの体積が求まります。

「コーンカップだけのポリゴン形状」(C)や「アイスクリームの乗ったコーンカップのポリゴン形状」（B）の体積はどうすれば求まるでしょう？それぞれのポリゴンは三角ポリゴンで構成されているので（されていない場合は仮想的にtriangulateします）、その三角ポリゴンに原点を加えた四面体の体積の和として求めることができます。

三角ポリゴンと原点からなる四面体

結局あるポリゴンオブジェクトを構成する各三角ポリゴンについて、その三角ポリゴンに原点を加えた四面体の体積を求めることができればそのポリゴンオブジェクトの体積を求めることができることになります。このような四面体の体積は以下の式で求まります。

三角ポリゴン各頂点の座標をそれぞれとすると

式の導出は少し面倒なので省きます。脚注に軽く説明を書きましたので興味のある方はそちらをご覧ください。この計算を行うとうまい具合に「コーンカップ」を構成する各三角ポリゴンでは体積がマイナスの値、「アイスクリームの乗ったコーンカップ」を構成する各三角ポリゴンでは体積がプラスの値となります。

これらの各faceを元に作った四面体の体積は負

これらの各faceを元に作った四面体の体積は正

ですので体積を求めたいポリゴンオブジェクトの全ての三角ポリゴンについてこの計算を行い、それらを足し合わせるとポリゴンオブジェクトの体積が求まります。原点はポリゴンオブジェクトの中にあっても外にあっても構いません。

簡単なPythonスクリプトでテストしてみましょう。この例では polyEvaluate()でfaceの数を調べ、0からface-1までのfaceが全て存在するものと仮定して.f[]でエッジ情報を取得していますが一般にはこの仮定は成り立たないのでご注意ください。

import maya.cmds as cmds

def getTriangeVerticesGenerator(polyName):
    for face in range(cmds.polyEvaluate(polyName, face=True)):
        cmds.select('%s.f[%d]' % (polyName, face), r=True)
        vertexIds = cmds.polyInfo(faceToVertex=True)[0].split()
        vertexIds = [int(x) for x in vertexIds if x.isdigit()]
        while len(vertexIds) >= 3:
            yield vertexIds[-3:]
            vertexIds.pop()

def getPolygonVolume(polyName):
    volume = 0.0
    for vertices in getTriangeVerticesGenerator(polyName):
        v1, v2, v3 = [cmds.pointPosition('%s.vtx[%d]' % (polyName, x), w=True) for x in vertices]    
        cross = v1[1]*v2[2] - v1[2]*v2[1], v1[2]*v2[0] - v1[0]*v2[2], v1[0]*v2[1] - v1[1]*v2[0]
        volume += (cross[0] * v3[0] + cross[1] * v3[1] + cross[2] * v3[2]) / 6.0
    return volume

使ってみると

cmds.polyCube()
print getPolygonVolume('pCube1')

実行結果
1.0

正しく求まっていますね。実際には原点からオブジェクトが離れすぎていると精度が落ちるので適当に（例えばオブジェクトの重心が原点に来るように）平行移動させた後この計算を行ったほうが良いでしょう。

（おまけ）Python Tips

getTriangeVertices()は普通の関数のように見えますがreturn文がなくその代わりに yieldが使われています。関数の中にyieldがあるものはジェネレータ関数と呼ばれます。ジェネレータ関数はその戻り値をfor文の中で使うことができます。

for vertices in getTriangeVertices(polyName):

このようにfor文を用いると、for文はyieldに渡されたオブジェクト（getTriangeVertices()の場合vertexIds[-3:]の値）を巡回するようになります。この関数が呼ばれると関数内の文はすぐには実行されず、for文などで値が必要になった場合に初めて実行されます。

例えば

def f():
    for val in range(4):
        yield val

for x in f():
    print x

実行結果
0
1
2
3

このスクリプトの動作は次のスクリプトと一見同じように見えますが

def f():
    vals = []
    for val in range(4):
        vals.append(val)
    return vals

for x in f():
    print x

実行結果
0
1
2
3

f()の中にprint文を入れて観察すると

def f():
    print 'f called'
    for val in range(4):
        print 'yielding ' + str(val)
        yield v

for x in f():
    print x

実行結果
f called
yielding 0
0
yielding 1
1
yielding 2
2
yielding 3
3

とfor文のループの度にf()の一部が実行されていることがわかります。

ジェネレータ関数は

・ メモリ節約のために大きな配列の要素をfor文で回す場合にその配列を予め用意したくない（10万オブジェクトの絶対パスを一つ一つ処理する場合など）

・ 予め配列を作っておくことができない（戻り値に時刻が入っている場合など）

のような場合に使われます。また複数の実行ラインを持ち、それらがお互いに協調しながらプログラムが実行されていくような特殊なプログラミング手法にも用いられているようです。

（三角錐の体積導出）

三角ポリゴン各頂点位置ベクトルをとし、原点、、を頂点とする三角形（図の青色の三角ポリゴン部分）を考えると、外積の大きさはこの三角形の面積の2倍、向きは法線方向となります。つまりこの三角形の面積を、法線の単位ベクトルをとすると、。四面体の体積はこのを底面積とする三角錐の体積なので、三角錐の体積の公式から高さをとすると。高さはとの内積となるので、

これを成分で書き下すと上述の式になります。

Vの符号はの符号によります。

##    [免責事項]
##        このソフトウェアの使用に関しては自己責任になります。
##        当社は何ら一切の責任を負いません。
##
##    [Terms of Use]
##        Use of this software is a self-responsibility.
##        Our company assumes no responsibility.