Main

TOP
DF TALK
math(数学)関数を自作しよう！

math(数学)関数を自作しよう！

2013/6/17

はじめまして、開発室の高山です。
自分は4月から入社したのですが、映像系ではなく情報系出身の人間ということもあり、MayaやAfterEffectsなどはまだまだ勉強中の身であります。
なので今回は 「math(数学)関数を自作しよう！」 といった情報・数学よりのテーマで語りたいと思います。

タイトルを見て頂ければ分かると思いますが、今回見応えのある画像や動画は一切出てきません。期待していた方ごめんなさい;;
後今回出てくるコードは全てC++で書かれたものです。

数学関数とは

math(数学)関数とは絶対値とか三角関数とか指数関数とか要するに数学的な処理をする時に使う関数です(ざっくり)。

「数学関数とか用意されているもの（標準ライブラリ）を使えばいいじゃん！」 と思われる方もいらっしゃるでしょうが、
これらを自作する事にはただの自己満足ではなく次のようなメリットが考えられます。

自作のメリット

仕様を把握できる(例外処理を決められる)
標準ライブラリでは有効桁数や例外処理などがどうなっているのかは外から見えず、調べないと分からない事が多いです。
またmath.hのfmod(剰余を求める関数)などは値によっては明らかに違う答えが返ってくる事もあり、それを知らないまま用いると原因不明のバグが起こりえます。
　
言語が変わっても同じ仕様を保つことができる
例えば0の0乗は言語によって返り値が異なります。中で標準ライブラリを呼び出しているプログラムを移植する場合、標準ライブラリの仕様が違うせいで結果が変わってしまった！というケースはないとは言えません。
自作関数だとそういう事態を防ぐことができます。
　
好きな型・引数で作ることができる
標準ライブラリだとintやdoubleなど決められた型でしか関数が作られておらず、さらにそれぞれ仕様が違います。
自作だと自分が定義した型で作ったり、特定の状況に合わせて引数の仕様や個数を変更したりできます。
　
必要とする有効桁数によって処理速度を変えられる
標準ライブラリはどの場合でも対応できるように有効桁数をかなり多めに取っていますが、そこまで必要ない場合は処理回数を減らすことができるので結果処理速度を速くする事ができます。
　
標準ライブラリよりも速くなる可能性がある
あくまで一例ですが、VisualC++のDebugモードだと絶対値計算はmath.hのfabsを呼び出すよりも自前で書いたほうが約10倍速くなる場合もあったりします。

もちろん仕様決め・関数作成・検証といった流れが面倒だったり、近似方法や計算方法を工夫しないと明らかに性能(精度・速度)が落ちてしまうといった問題もありますが、1回作ってしまえばずっと使い回せるということを考えれば作っておく価値は十分あると言えるでしょう。

では前置きをこれぐらいにしておいて実際に数学関数を自作してみましょう。
今回はsin(正弦)とsqrt(平方根)に焦点を当てたいと思います。

sin(正弦)関数の自作

sinやcos,expやlogなど多くの数学関数の近似にはマクローリン展開(テイラー展開)を利用できます。
詳しい説明は省きますが、例えばsinをマクローリン展開すると以下のような式になります。

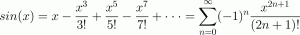
実際にコード化する場合は∞回の計算はもちろんできないので、これを適当な数にした上で落とし込むことになります。
これを踏まえてコード化したのがこちら。

#define PI 3.14159265358979323846

double my_sin(double x, int nMAX){
    x -= (int)(x / (2 * PI)) * 2 * PI; // -2π～2πにする

    double sum = x;// 合計値
    double t = x;

    for(int n=1;n<=nMAX;n++){
        t *= - (x * x) / ((2 * n + 1) * (2 * n));
        sum += t;
    }

    return sum;
}

基本は上の式をそのままコード化しただけですが、毎回累乗や階乗の計算をするのは時間がかかるので、
差分のみを掛け合わせて足すようにしています。
またxの値が大きくなると誤差が大きくなるので、xを-2π～2πの範囲に収まるように事前に変換しています。

nMAXでnの最大値(繰り返し回数)を設定できるようにしていますが、これは自分で調節して定数にしてもよいでしょう。
nMAXを増やすほど近似の精度が上がり、減らすほど計算時間の短縮ができるようになっています。

単純な実装だと上のようなわずか15行程度のコードで済んでしまいます。 簡単ですね！
cos(余弦)やtan(正弦)もそれぞれマクローリン展開してもいいのですが、sinさえ分かればそれを以下のコードのように公式を使って変換するだけで求められてしまいます。

double my_cos(double x, int nMAX){
    return my_sin(PI / 2 - x, nMAX);
}

double my_tan(double x, int nMAX){
    return my_sin(x, nMAX) / my_cos(x, nMAX);
}

いや～簡単ですね！(例外処理をしてないというのもありますが)

ただ多少複雑になったとしても精度や速度をもっと上げたいという要望ももちろんあると思います。
そこでテーブル引きといった手法を用いることにします。

テーブル引きによるsin関数の実装

テーブル引きとはある関数一定値ごとの答えをあらかじめテーブル(配列)として用意しておき、その間の値を補間や近似式で求めるといった手法です。例えばですが、0度、1度、2度…と1度ずつのsinの値を配列で用意しておき、1.4度など用意していない間の値は近似するということですね。
本来であれば用意できるテーブルの数には限りがあるので、与える引数にも上限や下限が出てきてしまいますが
(0～100までしかテーブルがなかった場合120.5などは求められない)、
幸いsin関数は2π周期なので2π分、さらに言えばπ/2分だけのデータを用意するだけで全ての引数で計算ができてしまいます。
それを踏まえたうえで、コードは以下のようになります。

#define PI 3.14159265358979323846
#define Data_num 90
// sinテーブル(0からπ/2までを90分割した時のsinの値)
const double sin_table[]={
0, 0.0174524064372835, 0.034899496702501, 0.0523359562429438,
0.0697564737441253, 0.0871557427476582, 0.104528463267653, 0.121869343405147,
0.139173100960065, 0.156434465040231, 0.17364817766693, 0.190808995376545,
0.207911690817759, 0.224951054343865, 0.241921895599668, 0.258819045102521,
0.275637355816999, 0.292371704722737, 0.309016994374947, 0.325568154457157,
0.342020143325669, 0.3583679495453, 0.374606593415912, 0.390731128489274,
0.4067366430758, 0.422618261740699, 0.438371146789077, 0.453990499739547,
0.469471562785891, 0.484809620246337, 0.5, 0.515038074910054,
0.529919264233205, 0.544639035015027, 0.559192903470747, 0.573576436351046,
0.587785252292473, 0.601815023152048, 0.615661475325658, 0.629320391049837,
0.642787609686539, 0.656059028990507, 0.669130606358858, 0.681998360062498,
0.694658370458997, 0.707106781186547, 0.719339800338651, 0.73135370161917,
0.743144825477394, 0.754709580222772, 0.766044443118978, 0.777145961456971,
0.788010753606722, 0.798635510047293, 0.809016994374947, 0.819152044288992,
0.829037572555042, 0.838670567945424, 0.848048096156426, 0.857167300702112,
0.866025403784439, 0.874619707139396, 0.882947592858927, 0.891006524188368,
0.898794046299167, 0.90630778703665, 0.913545457642601, 0.92050485345244,
0.927183854566787, 0.933580426497202, 0.939692620785908, 0.945518575599317,
0.951056516295154, 0.956304755963035, 0.961261695938319, 0.965925826289068,
0.970295726275996, 0.974370064785235, 0.978147600733806, 0.981627183447664,
0.984807753012208, 0.987688340595138, 0.99026806874157, 0.992546151641322,
0.994521895368273, 0.996194698091746, 0.997564050259824, 0.998629534754574,
0.999390827019096, 0.999847695156391, 1};

//関数本体
double my_sin_table(double x, int nMAX){
    int dir = 1;

    x /= PI;

    // 正の値にする
    if(x < 0){ 
        x = -x; 
        dir = -dir; 
    } 

    // 0～2πにする 
    x -= (int)(x / 2) * 2; 

    // 0～πにする 
    if(x > 1){
        x--;
        dir = -dir;
    }

    // 0～π/2にする
    if(x > 0.5) x = 1 - x;

    // xの値を0～90(Data_num)に補正
    x *= Data_num * 2;
    int a = (int)x;

    // テーブル引き(sin, cos両方)
    double si = sin_table[a];
    double co = sin_table[Data_num - a];
    double lx = (x - a) * PI / (Data_num * 2);

    // テイラー展開による近似補間
    double sum_si = 1;
    double sum_co = lx;
    double t = lx;

    for(int n=1;n<=nMAX;n++){
        t *= - lx / (n * 2);
        sum_si += t;
        t *= lx / (n * 2 + 1);
        sum_co += t;
    }

    return dir * (si * sum_si + co * sum_co);
}

引数を0～π/2に補正した後、テーブル引きをしてxの近辺aのデータ(sin(a) と cos(a))を取得します。
その近辺のデータをもとにテイラー展開で近似を行っています。
sinのテイラー展開は以下の式のようになっていて、sin(a)とcos(a)が分かればsin(x)を近似することができます。

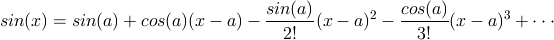
ちなみにこのaを0にすると上で述べたマクローリン展開の式になります。
コード上ではsin(a)をsi, cos(a)をco, (x – a)をlxで表しています。

今回は分割数を90(データの数を91個)にしましたが、この分割数を増やすほど精度は上がっていきます。
またnMAXで最後のテイラー展開の次数を変えることができます。普通の計算ならば2～3程度で充分でしょう。

分割数やnMAXの設定にもよりますが、基本的にはこちらのテーブル引きのほうが精度も速度も高くなります。
ただもちろんsinテーブルの精度に依存します。

sqrt(平方根)関数の自作

sinが長くなったのでsqrtは短めに。
平方根もマクローリン展開を使えることは使えるのですが、繰り返しをかなり大きくしないとなかなか収束しません。
そこでニュートン法を用いてより高速に近似することにします。

これも詳しい説明は省きますが、下の式のx₀に初期値(平方根を求めたい数)を入れてx_nをn=1,2,3,…と順番に求めていくと、
x_nがどんどん平方根の値に近づいていくような仕組みになっています。

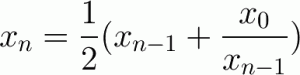
これをコード化したのがこちら。

double my_sqrt(double x, int nMAX){
    if(x <= 0) return 0;
    double t = x;

    for(int n=1;n<=nMAX;n++){
        t = (t + x / t) / 2;
    }

    return t;
}

負の値を入れたときは0が返ってくるようにしています。求める仕様によってNaNなどに変えてもいいでしょう。
またこれもnMAXでnの最大値(繰り返し回数)を設定できるようにしています。9、10あたりだとかなり正確な値が求められます。
自分は試していませんが、ニュートン法のかわりにハレー法やブレント法を用いればさらに高速化できるかもしれません。

いかがでしたでしょうか。
今回紹介した手法やコードはまだまだ発展の余地があるので、是非自分なりに工夫した数学関数を自作してみて下さい。
ただ精度や速度を求めすぎるとキリがなくなって他の作業が滞るのでほどほどに。

とりあえず絶対値や平方計算のようなすぐに作れてよく使う関数に関しては作っておいて損はないと思います。

※免責事項※
本記事内で公開している全ての手法・コードの有用性、安全性について、当方は一切の保証を与えるものではありません。
これらのコードを使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご使用ください。

コメントはありません

株式会社デジタル・フロンティア-Digital Frontier

Header