さて、弊社デジタルフロンティア(以下DF)のセットアップ室の主な業務は、Autodesk Mayaおよび
MotionBuilderでのキャラクターセットアップになります。弊社のセットアップ室はクロス、ヘアーの
仕込みからシミュレーションも担当します。地味に思われがちなセットアップ業務だけでなく、
最終的な絵作りにも関わることができるのはDFのメリットかなと感じます。
その分覚えることも多いですが、やりがいのある仕事です！

今回はエクスプレッションを用いた車のセットアップについて紹介したいと思います。
エクスプレッションとは、キャラクターセットアップやアニメーションの反復動作の効率化する為に使用されるMayaの機能です。DFのセットアップ室でも、特に人体セットアップ作業では使用頻度が高くなっています。そのほとんどは社内のツールで自動化されているので、全てを1から書くということはありませんが、セットアップでは必須のスキルですね。
パーティクルの制御にも用いられますが、今回はどちらかというとセットアップ寄りなので、ご了承ください。
エクスプレッションのような「文字」で作業することは始めはハードルが高く感じるかも。MelやPythonといったスクリプトの習得をしたいなーと、考えている方は、エクスプレッションから入ってみるのもいいかもしれませんよ。
簡単な数式で、アニメーションが作れたりとMayaの世界をより快適なものにしてくれるはずです。
　
　

エクスプレッションを用いた車のセットアップ：アジェンダ

1.タイヤの制御その1：コントローラーとの関連付け
2.タイヤの制御その2：距離に応じたタイヤの回転エクスプレッション
3.インタラクティブピボット：バンク(傾き)のコントロール
4.エクスプレッションの制御テクニック：WeightとOffset
5.おまけ：旋回の中心点を取得しよう
6.エクスプレッションのメリット/デメリット
7.まとめ

※動画のMayaのバージョンは2014を使用しています。
　

1.タイヤの制御その1：コントローラーとの関連付け

expression editor

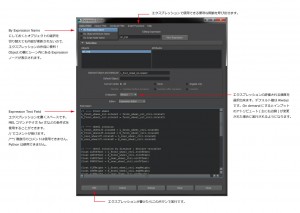
■エクスプレッション エディタ

エクプレッションを作成する時はメニューのウィンドウ＞アニメーション エディタ＞エクスプレッション エディタから起動します。
各項目は画像の通りです。エクスプレッションをメインで作業するときはフィルタの選択をエクプレッション名にしておくと現在の選択したノードに関わらずエクスプレッションが切り替わらないので、作業しやすいと思います。
　
　
　
　

■エクプレッションの使い方

エクスプレッションの一番基本的な使い方から始めましょう。一般的に↓この形から派生していきます。

ノード名.アトリビュート名 = ノード名.アトリビュート名;
　

car wheel expression : コントローラー名

// —- wheel rotation
L_front_wheelJT.rotateX = L_front_wheel_ctrl.rotateX;
R_front_wheelJT.rotateX = R_front_wheel_ctrl.rotateX;
L_rear_wheelJT.rotateX = L_rear_wheel_ctrl.rotateX;
R_rear_wheelJT.rotateX = R_rear_wheel_ctrl.rotateX;

という感じです。
　

ここで既に頭が痛い方いませんか？アルファベットや数字、演算子(=や＋ーの記号)に惑わされないようにしましょう。
右辺の内容(計算結果)が左辺に代入されるといった意味合いになります。きちんと意味を理解すれば大して難しいことは
書いていないことがすぐにわかると思います。行の最後は ; (セミコロン)で締めるのを忘れずに！

エクスプレッション内では // でコメントを書くことができます。計算には無視される文章ですね。
慣れないうちは説明文を残しておいて、後で確認できるようにしておくといいでしょう。
他人の方が引き継いだ時にも分かりやすくしておくと尚良いです。
　
　

2.タイヤの制御その2：距離に応じたタイヤの回転エクスプレッション

車の進んだ距離に応じてタイヤが自動で回転するエクスプレッションを書いていきます。ちょっと頭を使うところです。
エクスプレッションを書き始める前に計算式を考え、扱う情報を整理しましょう。

タイヤの円周と回転量について

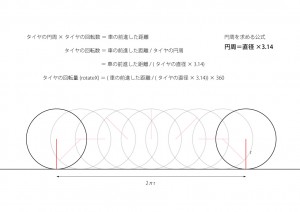
タイヤの円周 × タイヤの回転数 ＝ 車の前進した距離

とします。タイヤの円周を右辺に持って来て、

タイヤの回転数 ＝ 車の前進した距離 / タイヤの円周

となります。円の円周の公式は直径×円周率なので、

タイヤの回転数 ＝ 車の前進した距離 / (タイヤの直径 × 3.14)

となります。
　

タイヤの回転を制御するのですが、Mayaの中では「タイヤが何回転するか」というよりも
「タイヤのRotate値はいくつになるか」というように考えますね。1回転は360°なので、
rotateXの1°当たりに進む距離を導き出すには、

タイヤの回転量(rotateX) ＝ (車の前進した距離 / (タイヤの直径 × 3.14)) × 360

となります。実際のエクスプレッションで用いるアトリビュート名と記号で書いてみると、

// —- wheel rotation by distance
L_front_wheel_exp.rotateX = (all_ctrl.translateZ / (2*3.14))*360;
R_front_wheel_exp.rotateX = (all_ctrl.translateZ / (2*3.14))*360;
L_rear_wheel_exp.rotateX = (all_ctrl.translateZ / (2*3.14))*360;
R_rear_wheel_exp.rotateX = (all_ctrl.translateZ / (2*3.14))*360;

となります。all_ctrlを前後に動かしてみるとタイヤが自動で回転していますね。後退すると逆回転になります。
　
　

3.インタラクティブピボット：バンク(傾き)のコントロール

どんどんいきましょう。続いて車の傾きを制御してみましょう。
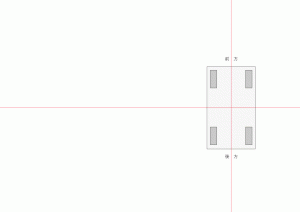
まずは、車がどの方向に傾くか監視するbank_pivot_directionというロケータに、bank_ctrlのrotate値を代入します。

// —- bank pivot direction
bank_pivot_direction.translateX = bank_ctrl.rotateZ * -1;
bank_pivot_direction.translateZ = bank_ctrl.rotateX;

傾いた方向にロケータが移動するようになりました。

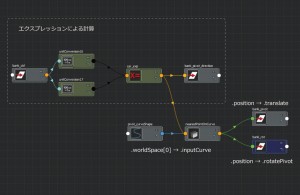
次にnearestPointOnCurveノードを使用します。nearestPointOnCurveノードはある一つのオブジェクトの位置からそのカーブの最も近いポイントの位置情報を取得できるノードです。pivot_curveShapeのworldSpace[0]とnearestPointOnCurve1のinputCurveにコネクションします。
　
　
続いて下記の様にエクプレッションを作成します。
vector $vはベクター型と呼ばれる変数です。三つの値をセットにして扱える型ですね。
.x.y.zでリストと同じように各要素を取り出すことができます。

// —– Nearest Point On Curve
vector $v = <<bank_pivot_direction.translateX, 0, bank_pivot_direction.translateZ>>;
nearestPointOnCurve.inPositionX = $v.x;
nearestPointOnCurve.inPositionY = $v.y;
nearestPointOnCurve.inPositionZ = $v.z;

nearestPointOnCurve.result.positionをbank_rotのrotatePivotに繋ぎます。
※bank_pivot.translateにも繋いでおくと位置を確認できます。

バンク(傾き)コントローラー名

nearestPointOnCurve：ノードコネクション

4.エクスプレッションの制御テクニック：WeightとOffset

エクスプレッションはいろいろ自動化できて非常に便利です。しかし、常に自動化された結果が正しいとは限りません。
演出で、エクスプレッションをOFFにして手付けでアニメーションを行いたいといった場面もでてきます。
そんな時に便利なので、ウェイトとオフセットという追加のアトリビュートです。
ウェイトはエクスプレッションの影響をどれだけ反映させるか調整できるアトリビュートで、
オフセットはエクスプレッションの結果に任意で上乗せ(または差し引く)ことができるアトリビュートになります。

2.の距離に応じたタイヤの回転エクスプレッションを例にとってみます。
各タイヤのコントローラーに Rot Offset と Exp Weight というアトリビュートを追加しました。
エクスプレッションを修正します。

// —- wheel rotation by distance : declare variables
float $LFOffset = L_front_wheel_ctrl.rotOffset;
float $RFOffset = R_front_wheel_ctrl.rotOffset;
float $LROffset = L_rear_wheel_ctrl.rotOffset;
float $RROffset = R_rear_wheel_ctrl.rotOffset;

float $LFWeight = L_front_wheel_ctrl.expWeight;
float $RFWeight = R_front_wheel_ctrl.expWeight;
float $LRWeight = L_rear_wheel_ctrl.expWeight;
float $RRWeight = R_rear_wheel_ctrl.expWeight;

// —- wheel rotation by distance
L_front_wheel_exp.rotateX = ((all_ctrl.translateZ / (2*3.14))*360) * $LFWeight + $LFOffset;
R_front_wheel_exp.rotateX = ((all_ctrl.translateZ / (2*3.14))*360) * $RFWeight + $RFOffset;
L_rear_wheel_exp.rotateX = ((all_ctrl.translateZ / (2*3.14))*360) * $LRWeight + $LROffset;
R_rear_wheel_exp.rotateX = ((all_ctrl.translateZ / (2*3.14))*360) * $RRWeight + $RROffset;
　
　
始めに追加した8つのfloat型の変数は各コントローラーからのアトリビュート値を代入しているだけです。
続くエクスプレッションが長く読みづらくなってしまうのを避けるためですが、気にならない方は

　
の4行でもOKです。
　
　

進行方向とタイヤの自動回転の向き

■all_ctrlの移動値と回転値の分割

all_ctrlのtranslateZの値をエクスプレッションで取得していると、all_ctrlが回転したとき進行方向がZ方向でない場合、計算結果異なり、予期せぬ方向にタイヤが回転を始めてしまいます。そこで回転だけのTransformノード(all_rot_cnst)と移動だけのTransformノード(all_pos_cnst)を用意し、ペアレント化を行います。それぞれにall_ctrlからOrient Constrain、Point Constrainを設定し、all_pos_cnstから移動値を取得すると回転にも対応したセットアップになります。
　
　
// —- wheel rotation by distance
L_front_wheel_exp.rotateX = ((all_pos_cnst.translateZ / (2*3.14))*360) * $LFWeight + $LFOffset;
R_front_wheel_exp.rotateX = ((all_pos_cnst.translateZ / (2*3.14))*360) * $RFWeight + $RFOffset;
L_rear_wheel_exp.rotateX = ((all_pos_cnst.translateZ / (2*3.14))*360) * $LRWeight + $LROffset;
R_rear_wheel_exp.rotateX = ((all_pos_cnst.translateZ / (2*3.14))*360) * $RRWeight + $RROffset;

5.おまけ：旋回の中心点を取得しよう

今回時間の関係でリグに組み込めなかったのですが、車の旋回の中心点を取得してみたいと思います。
一般的な乗用車であればハンドルを切ると前輪が傾き、車が左右に曲がることが可能です。そのタイヤの角度によって回転運動の基準軸を取得したいと思います。タイヤの角度と進む向きのギャップ(スリップアングル等というらしいですが。)などの要素は今回は考慮に入れず、単純に後輪軸の延長したラインと、前輪の中心から傾きに直行したラインの延長が交わる点、且つ、車体の中心(重心)から同じ距離横方向に伸ばした位置を旋回の軸としました。文字での説明よりも詳しくは図を参照してみてください。

前輪の角度と旋回の中心点

エクスプレッションを書く前にここでも先に情報の整理です。
前輪の傾きによって、前輪の中心、後輪の中心、そして上で定義したラインが交わる点で直角三角形ができます。
ここで不変の距離は、前輪の中心から後輪の中心までの距離なので、三角関数を用いて旋回の中心点を導きだすことができます。
　
　
←はGIFアニメーションです。クリックして下さい。
　
　
　

旋回の中心点までの距離 = 前輪の中心と後輪の中心の距離 × tan(※前輪の傾き)
※前輪の傾きはラジアンで指定する必要があります。

となります。実際のエクスプレッションでは

turn_pivot.translateX = 8 * tan(deg_to_rad(90 – front_wheel_rot_ctrl.rotateY));

となり、90 – front_wheel_rot_ctrl.rotateYで三角関数で用いられるθの部分の角度になります。
エクスプレッションのtan()関数では角度の単位にラジアンを用いる必要があるので、deg_to_rad()という
°(度)をラジアンに変換する関数があるので、こちらを使用しました。

※°(度)で計算できるtand()という関数もあります。その場合は
turn_pivot.translateX = 8 * tand(90 – front_wheel_rot_ctrl.rotateY);

となります。

ここで、括弧内が0°だった場合ですが、tan()関数は傾きなしになってしまい、turn_pivotは無限に遠くにいってしまいます。if文の条件式を使用して、傾きなしの場合は元の初期値に戻ってくるようにしましょう。
　
　
// —- Turn pivot position
if(front_wheel_rot_ctrl.rotateY == 0){
    turn_pivot.translateX = 0;
}else{
    turn_pivot.translateX = 8*tan(deg_to_rad(90-front_wheel_rot_ctrl.rotateY));
}
　
　
front_wheel_rot_ctrl.rotateY == 0 の場合 turn_pivot.translateX = 0 になります。
それ以外の場合は先に定義した式になります。
turn_pivot.translateX = 8*tan(deg_to_rad(90-front_wheel_rot_ctrl.rotateY));
　
　

6.エクスプレッションのメリット/デメリット

■エクスプレッションのメリット

　
・時間変化を利用したアニメーションの作成に便利
・反復、分岐の処理か容易
・テキストデータの為、作業の蓄積・共有が容易
・多くのアトリビュートにアクセスする場合や、複雑な処理もノード一つで可能
・アドリブが利きやすい

ドリブンキーやコンストレイン、ノードコネクションによる操作をエクスプレッションに置き換えることも可能です。
複数のノードを一つのエクスプレッションにまとめ、結果的にシーンを軽くすることもできるかもしれません。
また、文字での操作なので、作成したエクスプレッションは資産として残して再利用することも可能です。
不自由なく使える様になれば、アーティストの考えたものを直感的に作成できるパワフルな方法の一つになります。

個人的には最後のアドリブが利きやすいというのが大事ですね。仮でセットアップする際にエクスプレッションで
書いてみて確認する時に使いやすく感じています。思った方向に行かなかったときには-1を掛けてしまえとか。
スピーディーに対応できるところなどはメリットだと思います。
　
　

■エクスプレッションのデメリット

MotionBuilderに持っていく事ができません。MotionBuilderの中ではRelationという機能を用いて代用します。
DF内ではMotionBuilderを使用する機会が多いので、自動化されていない部分(自分で追加したエクスプレッションなど)はMotionBuilder内で再現する為の作業が発生してしまう場合があります。

アトリビュートをいくつでも纏めて管理できるので、逆にシーンを重くしてしまうことも。Alwaysの評価の方法は毎フレーム、エクスプレッションを計算します。その結果、必要の無い計算がボトルネックになってしまい、再生パフォーマンスが落ちてしまうことがあります。その場合はエクスプレッションノードを複数分けたり、代替の機能を検討する必要があるかもしれません。場合によっては評価の頻度をOn demandにしてアトリビュートにアクセスした場合のみ反映されるようにするのもいいかもしれません。
　
　

■エクスプレッションで記述する形

アトリビュートの値へのアクセスは = を使い、アトリビュートに直接代入することが推奨されています。
　
float $x = `getAttr pSphere1.translateX`;   // getAttr コマンドでpSphere1のtranslateXの値を取得
setAttr pCube.translateX $x;   // setAttr コマンドでpCubeのtranslateXの値に代入
　
のように、エクスプレッション内でMelコマンドを使用して値を取得代入が可能ですが、上記の内容なら
= を使って↓のように書くほうが処理が速くなります。
　
pCube.translateX = pSphere1.translateX;
　
　
Melコマンドを使う場合：単純なアトリビュート値の操作では難しい表現をする時に使用します。
時間によってオブジェクトが軌跡を追従する場合など、Melコマンド独自の機能を使って制御できます。
　
// pCube0のアニメーションをpCube1～pCube9が1フレームずつ遅れて追従するエクスプレッション
for($i=1; $i<9; $i++){     float $valT[] = `getAttr -t (frame - $i) pCube0.translate`;     float $valR[] = `getAttr -t (frame - $i) pCube0.rotate`;     float $valS[] = `getAttr -t (frame - $i) pCube0.scale`;     setAttr ("pCube" + $i + ".translate") $valT[0] $valT[1] $valT[2];     setAttr ("pCube" + $i + ".rotate") $valR[0] $valR[1] $valR[2];     setAttr ("pCube" + $i + ".scale") $valS[0] $valS[1] $valS[2]; } 　 　 また、=で記述したオブジェクトとそのエクスプレッションノードの間にはノードコネクションが作成されます。
ノードコネクションが作成されてしまうこと避けたい場合(他のコネクションと競合してしまう場合など）、
代わりの方法としてMelコマンドを使用することができます。Melコマンドで制御する場合はエクスプレッションノードとの間にノードコネクションは作成されません。

■まとめ

車というモデルを使ってエクスプレッションの紹介をしてきました。本当に自由度の高い機能なので、使えば使うだけ、効率的な使い方ができるようになります。さらに、学校で習ったような数学や物理の知識があるとより一層高度な使い方ができるはずです。今回の車のセットアップはテキストだけでは理解しづらいかと思いますので、動画も是非見てみてください。皆さんの日々の制作の一助になれば幸いです。
　
　
　
　
デジタルフロンティア CG部セットアップ室は渋谷の桜丘町のオフィスにあります。飲食店が多く、近くにはさくら通りや西郷山公園といった桜が楽しめるスポットがあります。社内見学も随時受け付けていますので、興味をお持ちの方は是非ご連絡ください。

西郷山公園：会社でお花見

さくら通り

ミニ四駆部が発足！

ミニ四駆部の活動

　
　
　
DFセットアップ室では、リギングアーティストを大募集中です。
一緒に魅力的な作品を作っていきましょう！詳しくは、下記の募集要項をご覧ください。

【 -セットアップ室-  リギングアーティスト】募集要項はこちら

 デジタルフロンティア お問い合わせフォームはこちら