空間フィルタリングを別の表色系で！
2015/2/16
こんにちは、開発部の高山です。
今回は画像処理をRGB以外の表色系で行うとどうなるかという話です。
画像処理の例として空間フィルタリングを扱っていこうと思います。
空間フィルタリングとは
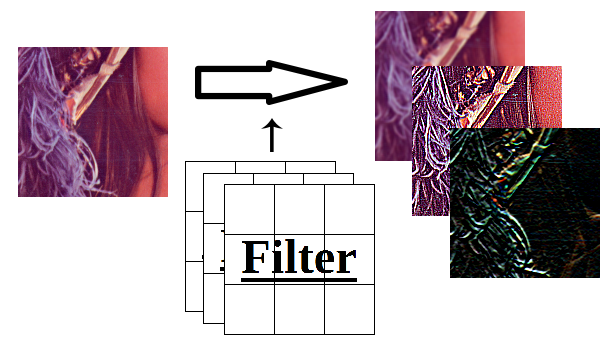
空間フィルタリングは画像処理でよく用いられる処理の１つで、
入力画像のピクセルごとに自身とその周囲のピクセルを使って計算することで様々な効果を与えるものです。
例えばぼかしやノイズ除去、エッジ抽出など、様々な用途に使うことができます。
では、実際に空間フィルタリングの計算方法を見ていってみましょう。
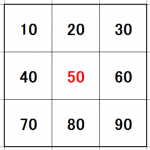
例えば、あるピクセルとのその周囲のピクセル値(例えば、RGBのR)が以下の画像のようだったとします。
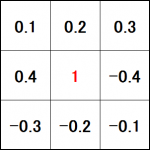
これにフィルタ(下画像)の対応する部分の数値を掛けていきます。
画像の例だと順番に 10×0.1, 20×0.2, 30×0.3, 40×0.4, 50×1, 60x(-0.4), 70x(-0.3), 80x(-0.2), 90x(-0.1) といった感じですね。
そしてこれらを足し合わせたものが出力結果となります。
この例ですと、(10×0.1) + (20×0.2) + (30×0.3) + (40×0.4) + (50×1) + (60x(-0.4)) + (70x(-0.3)) + (80x(-0.2)) + (90x(-0.1)) = 10 が結果となります。
これを全てのピクセル、RGBそれぞれに行っていくことで、空間フィルタリングを行った結果画像が得られます。
計算だけ見ても分かりにくいと思うので、実際にどういう効果を与えることができるのか見ていきましょう。
１．平滑化フィルタ(ぼかし効果)
最初の例ではフィルタに適当な値を入れて説明しましたが、これに特定の値を入れることで様々な効果を与えられます。
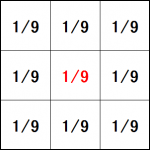
例えば以下のようなものに代表される平滑化フィルタを用いて計算を行うと、ぼかし効果のようなものが得られます。
結果はこんな感じに。上の画像が全体画像(クリックで拡大)で下の画像が一部を抽出したものになります。
| 入力画像 | 結果画像 |
 |
 |
 |
 |
範囲を広げたり、繰り返しフィルタをかけることで、より様々なぼかしを表現できます。
２．鮮鋭化フィルタ(シャープ化)
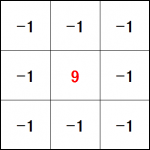
逆にシャープ化させるためには以下のような鮮鋭化フィルタを用います。
これを適用した例はこんな感じに。
| 入力画像 | 結果画像 |
|
 |
|
 |
計算結果が範囲外になる場合があるので注意しましょう。
３．ソーベルフィルタ(エッジ抽出)
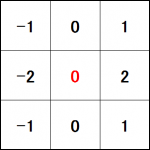
次は以下のようなフィルタ。これはソーベルフィルタと呼ばれるものの１つで、エッジ抽出を行う場合によく使われます。
結果はこんな感じ。
| 入力画像 | 結果画像 |
|
 |
|
 |
表色系とは
このような画像処理を行うときに、大半のプログラムやアルゴリズムではRGB表色系が用いられています。
RGB表色系はもちろんすぐれた表色系なのですが、輝度が分かりにくかったり、色差が等間隔でなかったりと欠点もあります。
そういうこともあり、他にも様々な表色系が提案されています。
今回はそれらの表色系について軽く触れ、それらを使って画像処理を行ったときにどういった違いが生じるかを検証してみました。
HSV表色系
HSV表色系はHSB表色系やHSI表色系とも呼ばれ、H(色相)・S(彩度)・V(明度)とそれぞれの成分の役割がはっきり分かれている所が特徴です。
HSVという名前にはピンとこなくても以下の画像のような色相環は見たことがある人は多いのではないでしょうか。
RGBよりも直観的に分かりやすいため、大抵のソフトでサポートされています。
Lab表色系
正確にはCIE-L*a*b*表色系などと呼ばれ、知覚的に均等である（人間が感じる色の違いの尺度が、距離として正しく計算される）ことを重視した表色系です。
Lが明度を表し、aとbで色を表現しています。
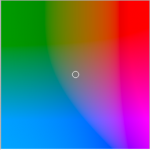
人間の知覚に沿って作られた表色系なので、成分ごとに範囲が違うなど分かりにくい部分はありますが、
色の距離を用いる場合はRGBよりもLabの方がより正しい結果が求められます。
結果
RGB表色系をHSV表色系、Lab表色系に変換したうえで空間フィルタリングするとどういう違いが出るかを実験してみました。
ただし、HSV表色系に関してはHを使うと色味がおかしくなってしまうため、HはそのままでSVのみ空間フィルタリングを行っています。
１．平滑化フィルタ(ぼかし効果)
|
 |
 |
| RGB表色系 | HSV表色系 | Lab表色系 |
２．鮮鋭化フィルタ(シャープ化)
|
 |
 |
| RGB表色系 | HSV表色系 | Lab表色系 |
３．ソーベルフィルタ(エッジ抽出)
|
 |
 |
| RGB表色系 | HSV表色系 | Lab表色系 |
平滑化フィルタは弱めのぼかしということもあってあまり違いは見られませんが、他の２つはそれなりに違いが出ています。
どの表色系がよりよい結果なのかは求めたいものによって変わってくるでしょう。
というか検証して分かったのですがRGBとLabの結果変わってないですね．．．＿|￣|○
より複雑なフィルタリングを行う場合は違いが出てくるはずですが、まあこれも１つの結果かと。
まとめ
今回主張したかったことを箇条書きにすると
・空間フィルタリングは１つのコードで色々な効果が得られてお得
・画像処理を実装するときにRGB以外の表色系も試してみては
・主張をするときは結果がともなわないと説得力に欠ける
こんなところで。では、また～。
おまけ
今回の画像生成に使ったコードの空間フィルタリング部分を載せておきます。
表色系の変換式は申し訳ありませんが長くなりすぎるので割愛。
const int SIZE = 1;
float WEIGHT[3][3][3] = {{{1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f}, {1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f}, {1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f}},
{{-1.0f, -1.0f, -1.0f}, {-1.0f, 9.0f, -1.0f}, {-1.0f, -1.0f, -1.0f}},
{{-1.0f, 0.0f, 1.0f}, {-2.0f, 0.0f, 2.0f}, {-1.0f, 0.0f, 1.0f}}};
float clamp(float x, float min, float max){
if(x < min) x = min;
if(x > max) x = max;
return x;
}
int mirror(int x, int min, int max){
while(x < min || x >= max){
if(x < min) x = min + (min - x - 1);
if(x >= max) x = max + (max - x - 1);
}
return x;
}
Color Pixel_Filter_RGB(Color *data, int x, int y, int width, int height, int method){
int MAX = 255;
int mx, my;
float w;
float r, g, b;
r = 0.0f;
g = 0.0f;
b = 0.0f;
for(int dy=-SIZE;dy<=SIZE;dy++){
for(int dx=-SIZE;dx<=SIZE;dx++){
mx = mirror(x + dx, 0, width);
my = mirror(y + dy, 0, height);
w = WEIGHT[method][dx + SIZE][dy + SIZE];
r += (float)data[mx + my * width].R / MAX * w;
g += (float)data[mx + my * width].G / MAX * w;
b += (float)data[mx + my * width].B / MAX * w;
}
}
r = clamp(r, 0.0f, 1.0f) * MAX;
g = clamp(g, 0.0f, 1.0f) * MAX;
b = clamp(b, 0.0f, 1.0f) * MAX;
return Color::FromArgb((int)r, (int)g, (int)b);
}
※免責事項※
本記事内で公開している全ての手法の有用性、安全性について、当方は一切の保証を与えるものではありません。
これらの手法を使用したことによって引き起こる直接的、間接的な損害に対し、当方は一切責任を負うものではありません。
自己責任でご活用ください
コメント
コメントフォーム